题目内容
(本小题满分12分)如图,四棱锥P?ABCD中,底面ABCD为平行四边形,O为AC的中点,PO⊥平面ABCD,M 为PD的中点,∠ADC = 45o,AD = AC = 1,PO=a

(1)证明:DA⊥平面PAC;
(2)如果二面角M?AC?D的正切值为2,求a的值.
(1)祥见解析;(2)a=2.
【解析】
试题分析:(1)由PO⊥平面ABCD,得PO⊥AD,由∠ADC=45°,AD=AC,得AD⊥AC,从而证明AD⊥平面PAC.(2)法一,先利用三垂线定理作出二面角M-AC-D的平面角:连结DO,作MG⊥DO于G,作GH⊥AO于H,因为M是PD中点,且MG⊥DO,所以G为DO中点,且MG⊥平面ABCD,显然,∠MHG即为二面角M-AC-D的平面角.然后在直角三角形MHG中,可用a表示出的正切值,从而由已知即可求出a的值;法二,以OA为x轴,OP为y轴,O为坐标原点建立空间直角坐标系,利用空间向量知亦可求.
试题解析: (1)证明:由题意,∠ADC = 45o,AD = AC = 1,故∠DAC = 90o
即DA⊥AC.又因为 PO⊥平面ABCD,
所以,DA⊥PO,DA⊥平面PAC 4分
(2)法一:连结DO,作MG⊥DO于G,作GH⊥AO于H,因为M是PD中点,且MG⊥DO,所以G为DO中点,且MG⊥平面ABCD,显然,∠MHG即为二面角M-AC-D的平面角. 8分

因为GH⊥AO,且G为DO中点,所以 ,而
,而 ,故
,故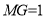 ,PO=2MG=2. 12分
,PO=2MG=2. 12分
法二:建立如图所示的空间直角坐标系O-xyz,则 ,
,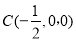 ,
,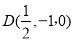 ,
,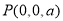 ,
,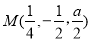

设平面MAC的法向量为 ,
,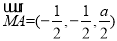 ,
, ,则
,则 ,所以
,所以 的一个取值为
的一个取值为
 10分
10分
平面ACD的法向量为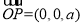 .
.
设二面角的平面角为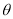 ,
,
因为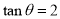 ,所以
,所以
a=2 12分
考点:1. 直线与平面垂直的判定;2二面角.

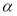 ,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).
,条件“直线l与平面α内的无数条直线都垂直”是“直线l与平面α垂直的( ).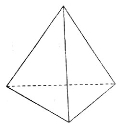
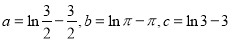 ,大小顺序正确的是( )
,大小顺序正确的是( )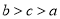 B.
B. C.
C. 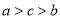 D.
D.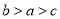
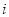 是虚数单位,则复数
是虚数单位,则复数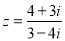 的虚部是( )
的虚部是( )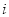 C.
C.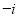 D.1
D.1 ,
, ,则
,则 的最小值为 ;
的最小值为 ;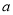 的正方形的四棱锥
的正方形的四棱锥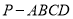 中,已知
中,已知 ,且
,且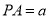 ,则直线
,则直线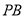 与平面
与平面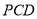 所成的角的余弦值为( )
所成的角的余弦值为( )
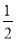 B.
B.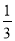 C.
C. D.
D.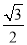
 ∶
∶ ∶
∶
 ∶
∶ ∶
∶ ,则角
,则角 .
.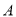 ,
,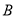 间的距离,某同学首先选定了与
间的距离,某同学首先选定了与 ,然后给出了四种测量方案:(△
,然后给出了四种测量方案:(△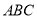 的角
的角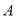 ,
,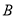 ,
,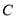 所对的边分别记为
所对的边分别记为 ,
,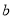 ,
,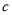 )
)
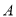 ,
,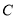 ,
,
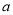 ,
,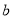 ,
,
 ,
, ,
,