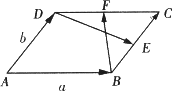
题目内容
如图所示,在
ABCD中,
=a,
=b,M是AB中点,点N是BD上一点,| 
|=
|
|.求证:M、N、C三点共线.
思路分析:将点共线问题转化成向量共线问题,即证明
=3
.
证明:∵=a,=b,∴=-=a-b.
∴
=
+
=
b+
=
b+
(a-b)=
a+
b=
(2a+b).
又∵
=
+
=
b+a=
(2a+b),
∴
=3
.
又
与
有共同起点,
∴M、N、C三点共线.
温馨提示
几何中证明三点共线,通常以三点为起点和终点确定两个向量,然后看能否找到唯一的实数λ,使得一个向量等于另一个向量的λ倍,把三点共线问题转化成向量共线的问题.
练习册系列答案
同步练习强化拓展系列答案
相关题目
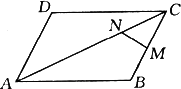
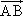＝a，
＝b，
＝3
，M为BC的中点，则
＝________．(用a、b表示)
＝a，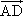
＝b，则以a，b为基底表示向量
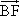为________，
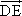为________．
ABCD中，已知
=a，
=b. 
、
；
ABCD为矩形.