题目内容
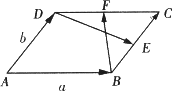
如图所示,在ABCD中,∠BCD=90°,BC=CD=1,AC⊥平面BCD,∠ADC=45°,E是线段AD的中点,F是线段AC上的一个动点.
(1)确定点F的位置,使平面ABD⊥平面BEF;
(2)当平面ABD⊥平面BEF时,求直线DB与EF所成的角.

解:(1)由已知可得AB=AD=BD=![]() ,又AE=ED,则BE⊥A D.
,又AE=ED,则BE⊥A D.
由平面ABD⊥平面BEF得AD⊥平面BEF,故AD⊥EF,
即F应为过点E的AD的垂线和AC的交点,由AC=CD知F点即为C点.
(2)由(1)知,EF与BD所成的角即为EC与BD所成的角.
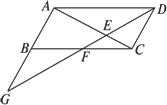
延长AC至G,使得CG=AC,连接DG,
则∠BDG即为CE与BD所成的角.
在△BDG中,BD=DG=BG,所以∠BDG=60°,
即直线EF与直线BD所成的角为60°.

练习册系列答案
相关题目
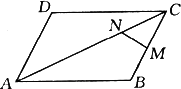
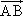 =a,
=a,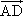 =b,则以a,b为基底表示向量
=b,则以a,b为基底表示向量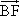 为________,
为________,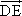 为________.
为________.