题目内容
已知函数 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 在区间
在区间 上的最大值为12.
上的最大值为12.
(1)求 的解析式;
的解析式;
(2)设函数 在
在 上的最小值为
上的最小值为 ,求
,求 的表达式.
的表达式.
(1) ;(2)①当
;(2)①当 ,即
,即 时,
时, ;
;
②当 时,
时, ;③当
;③当 ,即
,即 时,
时, .
.
解析试题分析:(1)由题意先设函数的解析式,再由条件解其中的未知数,可得二次函数解析式;(2)由(1)知函数的解析式,可得函数的对称轴为 ,再讨论对称轴是在区间
,再讨论对称轴是在区间 上,还是在区间外,分别得
上,还是在区间外,分别得 的表达式.
的表达式.
试题解析:(1)
 是二次函数,且
是二次函数,且 的解集是
的解集是
 可设
可设 2分
2分 在区间
在区间 上的最大值是
上的最大值是 由已知,得
由已知,得
 5分
5分 . 6分
. 6分
(2)由(1)知 ,开口向上,对称轴为
,开口向上,对称轴为 , 8分
, 8分
①当 ,即
,即 时,
时, 在
在 上是单调递减,
上是单调递减,
所以 ; 10分
; 10分
②当 时,
时, 在
在 上是单调递减,所以
上是单调递减,所以 ; 12分
; 12分
③当 ,即
,即 时,
时, 在对称轴处取得最小值,所以
在对称轴处取得最小值,所以 . 14分
. 14分
考点:1、二次函数的解析式的求法;2、二次函数的性质.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与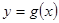 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.
 ;
; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的函数
的函数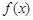 满足
满足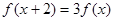 ,当
,当 ∈
∈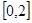 时,
时,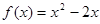
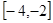 时,求
时,求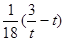 恒成立,求实数
恒成立,求实数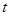 的取值范围.
的取值范围. 且
且 ,函数
,函数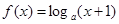 ,
,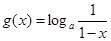 ,记
,记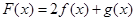 .
.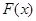 的定义域
的定义域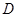 的表达式及其零点;
的表达式及其零点;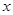 的方程
的方程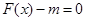 在区间
在区间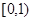 内仅有一解,求实数
内仅有一解,求实数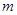 的取值范围.
的取值范围.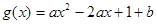 (
(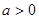 )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 ,
,  、
、 的值;
的值; 在
在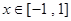 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.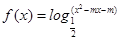 .
. )上是增函数,求实数m的取值范围.
)上是增函数,求实数m的取值范围.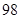 万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出
万元购置了一套生产设备并即刻生产产品,已知与生产产品相关的各种配套费用第一年需要支出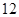 万元,第二年需要支出
万元,第二年需要支出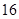 万元,第三年需要支出
万元,第三年需要支出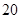 万元,……,每年都比上一年增加支出
万元,……,每年都比上一年增加支出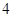 万元,而每年的生产收入都为
万元,而每年的生产收入都为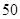 万元.假设这套生产设备投入使用
万元.假设这套生产设备投入使用 年,
年,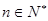 ,生产成本等于生产设备购置费与这
,生产成本等于生产设备购置费与这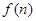 等于这
等于这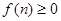 ,求
,求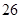 万元的价格出售该套设备;
万元的价格出售该套设备;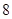 万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由.
万元的价格出售该套设备. 你认为哪个方案更合算?请说明理由. (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度 (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当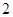 (千克/年);当
(千克/年);当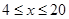 时,
时,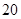 (尾/立方米)时,因缺氧等原因,
(尾/立方米)时,因缺氧等原因, (千克/年).
(千克/年).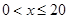 时,求函数
时,求函数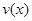 的表达式;
的表达式;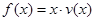 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.