题目内容
已知 且
且 ,函数
,函数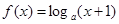 ,
,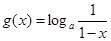 ,记
,记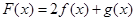 .
.
(Ⅰ)求函数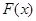 的定义域
的定义域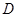 的表达式及其零点;
的表达式及其零点;
(Ⅱ)若关于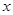 的方程
的方程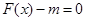 在区间
在区间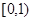 内仅有一解,求实数
内仅有一解,求实数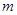 的取值范围.
的取值范围.
(Ⅰ)0;(Ⅱ)若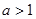 ,则
,则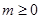 ,;若
,;若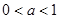 ,则
,则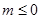 .
.
解析试题分析:(Ⅰ)先求函数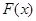 的定义域,注意对数的真数为正,分数的分母为正,由
的定义域,注意对数的真数为正,分数的分母为正,由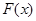
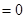 ,变为两个对数式相等,则两个真数等,便有
,变为两个对数式相等,则两个真数等,便有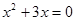 解方程即得,注意有无增根;(Ⅱ)用分离系数法变成
解方程即得,注意有无增根;(Ⅱ)用分离系数法变成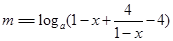 ,把对数式转换为指数式,利用函数
,把对数式转换为指数式,利用函数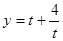 的性质求解.
的性质求解.
试题解析:(Ⅰ)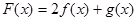
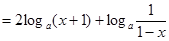 (
(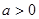 且
且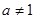 )
)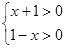 ,解得
,解得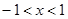 ,所以函数
,所以函数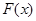 的定义域为
的定义域为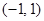 ,
,
令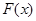
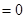 ,则
,则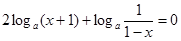 ……(*)方程变为
……(*)方程变为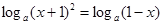 ,
,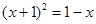 ,即
,即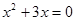 ,(3分)
,(3分)
解得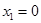 ,
,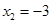 ,
,
经检验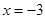 是(*)的增根,所以方程(*)的解为
是(*)的增根,所以方程(*)的解为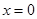 ,
,
所以函数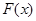 的零点为
的零点为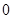 . (6分)
. (6分)
(Ⅱ)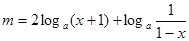 (
( )
)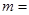
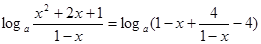 ,
,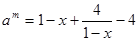 ,
,
设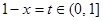 ,则函数
,则函数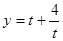 在区间
在区间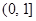 上是减函数, (9分)
上是减函数, (9分)
当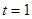 时,此时
时,此时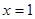 ,
, ,所以
,所以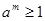 ,
,
①若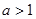 ,则
,则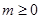 ,方程有解;
,方程有解;
②若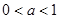 ,则
,则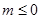 ,方程有解. (12分)
,方程有解. (12分)
考点:函数的零点,分类讨论.

练习册系列答案
相关题目
 的解集为M.
的解集为M. ,求实数
,求实数 的取值范围;
的取值范围; ,求实数
,求实数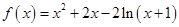 .
. 的单调区间;
的单调区间; 时,是否存在整数
时,是否存在整数 ,使不等式
,使不等式 恒成立?若存在,求整数
恒成立?若存在,求整数 的方程
的方程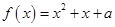 在
在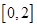 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数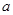 的取值范围.
的取值范围.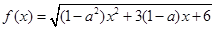 .若
.若 的定义域为
的定义域为 ,求实数
,求实数 的取值范围.
的取值范围. 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在 上,设矩形
上,设矩形 ,
,
 ,将
,将 的函数关系式;
的函数关系式; ,将
,将 的函数关系式;
的函数关系式; 是二次函数,不等式
是二次函数,不等式 的解集是
的解集是 ,且
,且 上的最大值为12.
上的最大值为12. 上的最小值为
上的最小值为 ,求
,求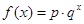 ;②
;②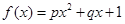 ;③
;③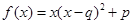 .(以上三式中
.(以上三式中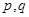 均为常数,且
均为常数,且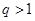 )
)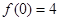 ,
,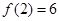 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是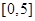 .其中
.其中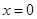 表示8月1日,
表示8月1日,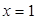 表示9月1日,…,以此类推);
表示9月1日,…,以此类推); 千件,需另投入成本为
千件,需另投入成本为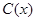 ,当年产量不足80千件时,
,当年产量不足80千件时, (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (万元)关于年产量
(万元)关于年产量 人,(
人,( ,且
,且 为偶数),每人每年可创利
为偶数),每人每年可创利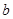 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?