题目内容
已知α,β都是锐角,sinα=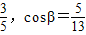 ,求 sin(α+β)的值.
,求 sin(α+β)的值.
【答案】分析:根据α,β都是锐角,sinα与cosβ的值,利用同角三角函数间的基本关系求出cosα与sinβ的值,所求式子利用两角和与差的正弦函数公式化简后,将各自的值代入计算即可求出值.
解答:解:∵α,β都是锐角,sinα= ,cosβ=
,cosβ=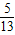 ,
,
∴cosα=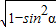 =
= ,sinβ=
,sinβ=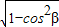 =
=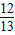 ,
,
则sin(α+β)=sinαcosβ+cosαsinβ= ×
×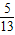 +
+ ×
×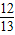 =
=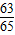 .
.
点评:此题考查了两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.
解答:解:∵α,β都是锐角,sinα=
 ,cosβ=
,cosβ=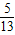 ,
,∴cosα=
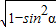 =
= ,sinβ=
,sinβ=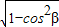 =
=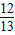 ,
,则sin(α+β)=sinαcosβ+cosαsinβ=
 ×
×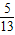 +
+ ×
×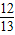 =
=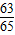 .
.点评:此题考查了两角和与差的正弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
 ,(1+tanA)(1+tanB)=2,求证A+B=45°.
,(1+tanA)(1+tanB)=2,求证A+B=45°.