题目内容
2.已知正四棱锥S-ABCD所有棱长为4,E是侧棱SC上一点,且SE=1,过点E垂直于SC的平面截该正四棱锥,则该平面与这个正四棱锥的截面面积为( )| A. | 8$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 5$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 取SC的中点M,连接BM、DM、BD,得出SC⊥平面BDM;
过点E作EF∥BM,EI∥DM,分别交SB、SD于点F、I,
分别取AB、AD的中点G、H,连接FG、GH、HI,
则SC⊥平面EFGHI,五边形EFGHI是过点E垂直于SC的平面截面图形,
计算截面面积即可.
解答 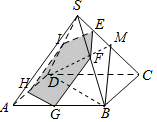 解:取SC的中点M,连接BM、DM、BD,如图所示,
解:取SC的中点M,连接BM、DM、BD,如图所示,
则SC⊥BM,SC⊥DM,
∴SC⊥平面BDM;
过点E作EF∥BM,EI∥DM,分别交SB、SD于点F、I,
分别取AB、AD的中点G、H,连接FG、GH、HI,
则GH∥BD,FG∥SA,HI∥SA,
∴SC⊥平面EFGHI,
∴五边形EFGHI是过点E垂直于SC的平面截面图形,
则截面面积为S截面EFGHI=2$\sqrt{2}$×2+$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{{(\sqrt{3})}^{2}{-(\sqrt{2})}^{2}}$=5$\sqrt{2}$.
故选:C.
点评 本题考查了正棱锥的定义与应用问题,也考查了几何体面积的求法以及空间想象能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 某多面体的三视图如图所示,则该多面体最短的一条棱长为( )
某多面体的三视图如图所示,则该多面体最短的一条棱长为( )
 某多面体的三视图如图所示,则该多面体最短的一条棱长为( )
某多面体的三视图如图所示,则该多面体最短的一条棱长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |