题目内容
设函数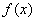 和
和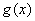 都是定义在集合
都是定义在集合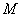 上的函数,对于任意的
上的函数,对于任意的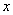
 ,都有
,都有
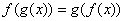 成立,称函数
成立,称函数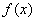 与
与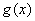 在
在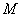 上互为“
上互为“ 函数”.
函数”.
(1)函数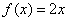 与
与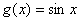 在
在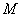 上互为“
上互为“ 函数”,求集合
函数”,求集合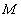 ;
;
(2)若函数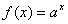 (
(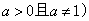 与
与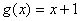 在集合
在集合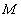 上互为 “
上互为 “ 函数”,
函数”,
求证: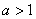 ;
;
(3)函数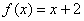 与
与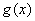 在集合
在集合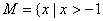 且
且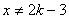 ,
,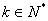
 上互为“
上互为“ 函数”,当
函数”,当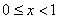 时,
时,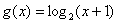 ,且
,且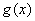 在
在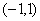 上是偶函数,求函数
上是偶函数,求函数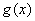 在集合
在集合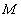 上的解析式.
上的解析式.
(1)由 得
得 化简得,
化简得, ,
, 或
或
解得 或
或 ,
, ,即集合
,即集合

(若学生写出的答案是集合 的非空子集,扣1分,以示区别。)
的非空子集,扣1分,以示区别。)
(2)证明:由题意得, (
( 且
且 )变形得,
)变形得, ,由于
,由于 且
且
 因为
因为 ,所以
,所以 ,即
,即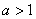
(3)当 ,则
,则 ,由于函数
,由于函数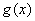 在
在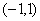 上是偶函数
上是偶函数
则 所以当
所以当 时,
时,
由于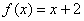 与函数
与函数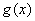 在集合
在集合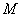 上“ 互为
上“ 互为 函数”
函数”
所以当 ,
, 恒成立,
恒成立, 对于任意的
对于任意的 (
( )恒成立,即
)恒成立,即
所以 ,即
,即
所以 ,当
,当 (
( )时,
)时,

所以当 时,
时,
 ………2分
………2分

练习册系列答案
相关题目
 D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )
D四个不同的岗位服务,每个岗位至少有一名志愿者,则甲和乙不在同一岗位服务的概率为( )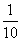 (B)
(B) 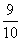 (C)
(C) 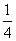
 (D)
(D) 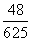
 图象上关于坐标原点
图象上关于坐标原点 对称的点有
对称的点有 对,则
对,则 的值为( )
的值为( ) ,其中
,其中 ,若动直线
,若动直线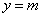 与函数
与函数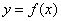 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 ,则
,则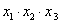 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”_______________. ,
, (0,π),则
(0,π),则 =( )
=( ) B -1 C
B -1 C  D 1
D 1 在点(1,1)处的切线方程为 .
在点(1,1)处的切线方程为 . ·
· 且前n项和
且前n项和 ,则项数n等于 ( )
,则项数n等于 ( ) ”是“
”是“ ”的
”的