题目内容
(本小题满分12分)
设函数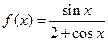 。
。
(Ⅰ)求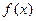 的单调区间;
的单调区间;
(Ⅱ)如果对任何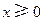 ,都有
,都有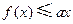 ,求
,求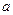 的取值范围。
的取值范围。
设函数
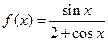 。
。(Ⅰ)求
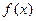 的单调区间;
的单调区间;(Ⅱ)如果对任何
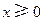 ,都有
,都有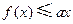 ,求
,求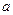 的取值范围。
的取值范围。(Ⅰ)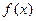 在每一个区间
在每一个区间 (
( )是增函数,
)是增函数,
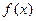 在每一个区间
在每一个区间 (
( )是减函数。
)是减函数。
(Ⅱ)
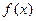 在每一个区间
在每一个区间 (
( )是增函数,
)是增函数,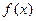 在每一个区间
在每一个区间 (
( )是减函数。
)是减函数。 (Ⅱ)

(Ⅰ)
 。 2分
。 2分当
 (
( )时,
)时, ,即
,即 ;
;当
 (
( )时,
)时, ,即
,即 。
。因此
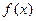 在每一个区间
在每一个区间 (
( )是增函数,
)是增函数,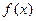 在每一个区间
在每一个区间 (
( )是减函数。 6分
)是减函数。 6分(Ⅱ)令
 ,则
,则

 。
。故当
 时,
时, 。
。又
 ,所以当
,所以当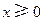 时,
时, ,即
,即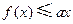 。 9分
。 9分当
 时,令
时,令 ,则
,则 。
。故当
 时,
时, 。
。因此
 在
在 上单调增加。
上单调增加。故当
 时,
时, ,
,即
 。
。于是,当
 时,
时, 。
。当
 时,有
时,有 。
。因此,
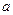 的取值范围是
的取值范围是 。 12分
。 12分
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
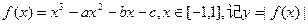 的最大值为M。
的最大值为M。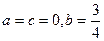 时,求M的值。
时,求M的值。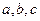 取遍所有实数时,求M的最小值
取遍所有实数时,求M的最小值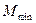 ;
;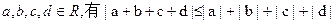 ,当
,当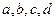 同号时取等号)
同号时取等号)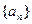 满足
满足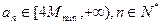 ,求证:
,求证: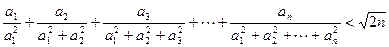 。
。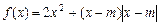 ,
,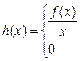
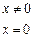 .
.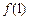 ≥4,求m的取值范围;
≥4,求m的取值范围;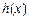 在
在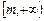 上是单调递增函数;
上是单调递增函数;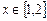 ,不等式
,不等式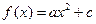 的图象经过点
的图象经过点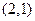 ,且在
,且在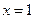 处的切线方程是
处的切线方程是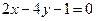
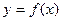 的解析式;
的解析式;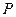 是直线
是直线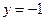 上的动点,自点
上的动点,自点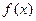 的图象的两条切线
的图象的两条切线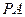 、
、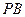 (点
(点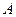 、
、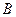 为切点),求证直线
为切点),求证直线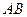 经过一个定点,并求出定点的坐标。
经过一个定点,并求出定点的坐标。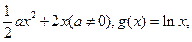
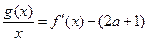 在区间
在区间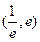 内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。
内有且只有两个不相等的实数根?若存在,求出a的取值范围?若不存在,请说明理由。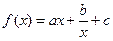 (
(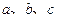 是常数)是奇函数,且满足
是常数)是奇函数,且满足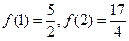 ,
,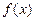 在区间
在区间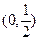 上的单调性并说明理由;
上的单调性并说明理由;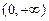 上的最小值.
上的最小值.
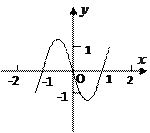 已知函数
已知函数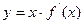 的图像如右图所示(其中
的图像如右图所示(其中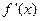 是函数
是函数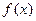 的导函数),下面四个图像中
的导函数),下面四个图像中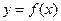 的图像大致是( )
的图像大致是( )
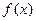 是偶函数,当
是偶函数,当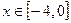 时.
时.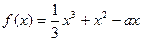 (a为实数).
(a为实数).
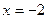 处有极值,求a的值。(6分)
处有极值,求a的值。(6分)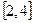 上是减函数,求a的取值范围。(8分)
上是减函数,求a的取值范围。(8分)