题目内容
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1,F2,以F2为圆心与双曲线的渐近线相切,若圆F2和双曲线的一个交点为M,满足MF1⊥MF2,则双曲线的离心率是$\frac{5}{3}$.分析 设F(c,0),渐近线方程为y=$\frac{b}{a}$x,运用点到直线的距离公式可得焦点到渐近线的距离为b,即为圆F的半径,再由MF1⊥MF2,结合双曲线的定义,利用勾股定理建立方程关系,运用a,b,c的关系和离心率公式,即可得到所求值.
解答 解:设F2(c,0),渐近线方程为y=$\frac{b}{a}$x,
可得F2到渐近线bx-ay=0的距离d=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
即圆F2的半径为b,
∵圆F2和双曲线的一个交点为M,
∴MF1-MF2=2a,MF2=b,
∴MF1=2a+b,
∵MF1⊥MF2,
∴MF12+MF22=F1F22,
即(2a+b)2+b2=4c2=4a2+4b2,
则4a2+4ab+b2=4a2+4b2,
即4ab=3b2,
则4a=3b,
则$\frac{b}{a}$=$\frac{4}{3}$,
即离心率e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{1+\frac{16}{9}}$=$\sqrt{\frac{25}{9}}$=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 本题考查双曲线的离心率的求法,注意运用点到直线的距离公式,利用双曲线的定义结合离心率的定义进行转化是解决本题的关键.

练习册系列答案
相关题目
2.在运行如图所示的程序框图,则输出的结果是( )


| A. | 30 | B. | 62 | C. | 126 | D. | 278 |
9.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)在左顶点与抛物线y2=2px(p>0)的焦点的距离为5,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-3,-6),则双曲线的焦距为( )
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{5}$ |
4.已知3x=2,3y=4,3z=8,则x,y,z为( )
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 既是等差,又是等比数列 | D. | 都不是 |
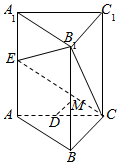 如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.
如图,直棱柱ABC-A1B1C1中,AB=AC=2,AA1=BC=2$\sqrt{3}$,E是AA1中点,D是AC的中点,M是BB1上一点,若DM∥平面B1CE,则$\frac{BM}{M{B}_{1}}$=3.