题目内容
已知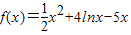 ,f′(x)是f(x)的导数.
,f′(x)是f(x)的导数.(Ⅰ)求y=f(x)的极值;
(Ⅱ)求f′(x)与f(x)单调性相同的区间.
【答案】分析:(I)由导数运算法则知,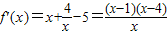 ,再利用导数与单调性关系求出极值即可;
,再利用导数与单调性关系求出极值即可;
(Ⅱ)求出函数f′(x)的导函数,在定义域下令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.
再结合(I)即可得到f′(x)与f(x)单调性相同的区间.
解答:解:(Ⅰ)∵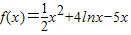 ,∴
,∴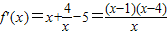 (x>0),
(x>0),
由f'(x)>0得,0<x<1或x>4,由f'(x)<0得,1<x<4.当x变化时,f'(x)、f(x)变化情况如下表:
∴f(x)的极大值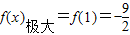 ,f(x)的极小值f(x)极小=f(4)=8ln2-12.…6分
,f(x)的极小值f(x)极小=f(4)=8ln2-12.…6分
(Ⅱ)设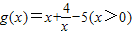 ,∴
,∴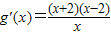 ,
,
由g'(x)>0得,x>2,g(x)为增函数,由g'(x)<0得,0<x<2,g(x)为减函数.
再结合(Ⅰ)可知:f'(x)与f(x)的相同减区间为[1,2],相同的增区间是[4,+∞)…12分.
点评:本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.
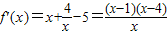 ,再利用导数与单调性关系求出极值即可;
,再利用导数与单调性关系求出极值即可;(Ⅱ)求出函数f′(x)的导函数,在定义域下令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.
再结合(I)即可得到f′(x)与f(x)单调性相同的区间.
解答:解:(Ⅰ)∵
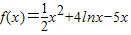 ,∴
,∴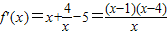 (x>0),
(x>0),由f'(x)>0得,0<x<1或x>4,由f'(x)<0得,1<x<4.当x变化时,f'(x)、f(x)变化情况如下表:
| x | (0,1) | 1 | (1,4) | 4 | (4,+∞) |
| f'(x) | + | - | + | ||
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
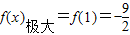 ,f(x)的极小值f(x)极小=f(4)=8ln2-12.…6分
,f(x)的极小值f(x)极小=f(4)=8ln2-12.…6分(Ⅱ)设
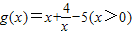 ,∴
,∴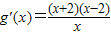 ,
,由g'(x)>0得,x>2,g(x)为增函数,由g'(x)<0得,0<x<2,g(x)为减函数.
再结合(Ⅰ)可知:f'(x)与f(x)的相同减区间为[1,2],相同的增区间是[4,+∞)…12分.
点评:本题主要考查导数与函数单调性的关系,会熟练运用导数解决函数的极值问题.求函数的单调区间,应该先求出函数的导函数,令导函数大于0得到函数的递增区间,令导函数小于0得到函数的递减区间.

练习册系列答案
相关题目
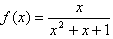 ;⑤f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f(x1)-f(x2)|≤2|x1-x2|。其中是F函数的序号为
;⑤f(x)是定义在R上的奇函数,且满足对一切实数x1,x2均有|f(x1)-f(x2)|≤2|x1-x2|。其中是F函数的序号为