题目内容
18.若${∫}_{0}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx=π(a>0),则实数a的值为2.分析 根据定积分的几何意义可知,${∫}_{0}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx表示以原点为圆心,以a为半径的圆的面积的四分之一,故${∫}_{0}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx=$\frac{1}{4}$πa2=π,问题得以解决.
解答 解:根据定积分的几何意义可知,${∫}_{0}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx表示以原点为圆心,以a为半径的圆的面积的四分之一,
故${∫}_{0}^{a}$$\sqrt{{a}^{2}-{x}^{2}}$dx=$\frac{1}{4}$πa2=π,
所以a=2,
故答案为:2.
点评 本题考查了定积分几何意义,属于基础题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
13.若C${\;}_{n}^{2}$=C${\;}_{n-1}^{2}$+C${\;}_{n-1}^{3}$(n∈N*),则($\root{3}{x}$-$\frac{1}{2\sqrt{x}}$)n的常数项为( )
| A. | -6 | B. | 12 | C. | $\frac{5}{2}$ | D. | -$\frac{5}{2}$ |
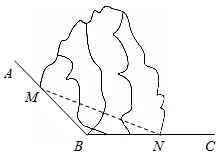 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).