题目内容
【题目】已知椭图![]() :
:![]() 的右顶点与抛物线
的右顶点与抛物线![]() :
:![]() 的焦点重合,椭圆
的焦点重合,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 且垂直于
且垂直于![]() 轴的直线截抛物线所得的弦长为
轴的直线截抛物线所得的弦长为![]() .
.
(1)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() .当直线
.当直线![]() 绕点
绕点![]() 旋转时,直线
旋转时,直线![]() 是否经过一定点?请判断并证明你的结论.
是否经过一定点?请判断并证明你的结论.
【答案】(1)![]() ,
, ![]() ;(2)是,证明见解析.
;(2)是,证明见解析.
【解析】
(1)利用椭圆的顶点与抛物线的焦点坐标相同,椭圆的离心率,列出方程组,求出![]() ,
,![]() ,即可得到椭圆方程抛物线方程;
,即可得到椭圆方程抛物线方程;
(2)把直线方程与椭圆方程联立可得根与系数的关系,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求得直线
,求得直线![]() 的方程,化简整理,由直线恒过定点的求法,可得所求定点.
的方程,化简整理,由直线恒过定点的求法,可得所求定点.
解:(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,依题意,可得
,依题意,可得![]() ,则
,则![]() :
:![]() ,
,
代入![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
则有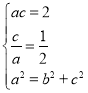 ,
,![]() .
.
所以椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
(2)依题意,当直线![]() 的斜率不为0时,设其方程为
的斜率不为0时,设其方程为![]() ,
,
联立![]() ,得
,得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ,
,
且![]() ,
,![]() ,
,
根据椭圆的对称性可知,若直线![]() 过定点,此定点必在
过定点,此定点必在![]() 轴上,设此定点为
轴上,设此定点为![]() ,
,
因斜率![]() ,得
,得![]() ,即
,即![]() ,
,
即![]() ,即
,即![]() ,
,
即![]() ,得
,得![]() ,
,
由![]() 的任意性可知
的任意性可知![]() .
.
当直线![]() 的斜率为0时,直线
的斜率为0时,直线![]() 的方程即为
的方程即为![]() ,也经过点
,也经过点![]() ,
,
所以当![]() 或
或![]() 时,直线
时,直线![]() 恒过一定点
恒过一定点![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知鲜切花![]() 的质量等级按照花枝长度
的质量等级按照花枝长度![]() 进行划分,划分标准如下表所示.
进行划分,划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花![]() ,现从两个种植基地购进的鲜切花
,现从两个种植基地购进的鲜切花![]() 中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
中分别随机抽取30个样品,测量花枝长度并进行等级评定,所抽取样品数据如图所示.
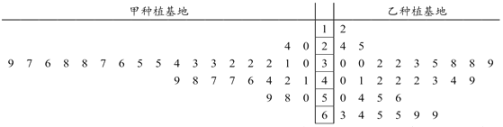
(1)根据茎叶图比较两个种植基地鲜切花![]() 的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
的花枝长度的平均值及分散程度(不要求计算具体值,给出结论即可);
(2)若从等级为三级的样品中随机选取2个进行新产品试加工,求选取的2个全部来自乙种植基地的概率;
(3)根据该加工企业的加工和销售记录,了解到来自乙种植基地的鲜切花![]() 的加工产品的单件利润为4元;来自乙种植基地的鲜切花
的加工产品的单件利润为4元;来自乙种植基地的鲜切花![]() 的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
的加工产品的单件成本为10元,销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花![]() 加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花
加工产品的保鲜特点,未售出的产品均可按原售价的50%处理完毕.用样本估计总体,如果仅从单件产品的利润的角度考虑,该鲜切花加工企业应该从哪个种植基地购进鲜切花![]() ?
?
【题目】通过随机询问200名性别不同的大学生是否爱好踢毽子运动,计算得到统计量![]() 的观测值
的观测值![]() ,参照附表,得到的正确结论是( )
,参照附表,得到的正确结论是( )
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
A.有97.5%以上的把握认为“爱好该项运动与性别有关”
B.有97.5%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过5%的前提下,认为“爱好该项运动与性别无关”