题目内容
(本小题满分12分)
已知{an}是递增的等差数列,满足a2·a4=3,a1+a5="4."
(1) 求数列{an}的通项公式和前n项和公式;
(2) 设数列{bn}对n∈N*均有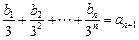 成立,求数列{bn}的通项
成立,求数列{bn}的通项 公式.
公式.
已知{an}是递增的等差数列,满足a2·a4=3,a1+a5="4."
(1) 求数列{an}的通项公式和前n项和公式;
(2) 设数列{bn}对n∈N*均有
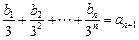 成立,求数列{bn}的通项
成立,求数列{bn}的通项 公式.
公式. 解:(1) ∵a1+a5=a2+a4=4,再由a2·a4="3,"
可解得a2=1,a4=3或a2= 3,a4=1(舍去)…………………………………………………3分
3,a4=1(舍去)…………………………………………………3分

 ………………………………………………………6分
………………………………………………………6分
(2) 由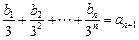 ,当n≥2时
,当n≥2时 ,
,
两式相减得 ………………………………………8分
………………………………………8分
∴bn=3n(n≥2)…………………………………………………………10分
当n=1时, ,
,
 .………………………………………………………12分
.………………………………………………………12分
可解得a2=1,a4=3或a2=
 3,a4=1(舍去)…………………………………………………3分
3,a4=1(舍去)…………………………………………………3分
 ………………………………………………………6分
………………………………………………………6分(2) 由
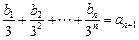 ,当n≥2时
,当n≥2时 ,
,两式相减得
 ………………………………………8分
………………………………………8分∴bn=3n(n≥2)…………………………………………………………10分
当n=1时,
 ,
, .………………………………………………………12分
.………………………………………………………12分略

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
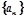 是公差不为0的等差数列,
是公差不为0的等差数列,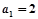 且
且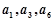 成等比数列,则
成等比数列,则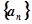 的前
的前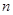 项和
项和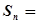
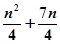
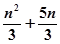
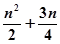
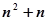
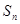 是等差数列
是等差数列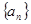 的前
的前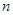 项和,若
项和,若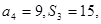 ,则数列
,则数列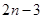
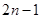
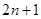
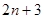
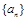 的前
的前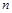 项和为
项和为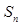 ,且
,且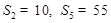 ,则过点
,则过点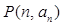 和
和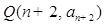
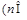 N*)的直线的斜率是
N*)的直线的斜率是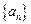 的前
的前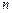 项和为
项和为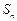 ,且满足
,且满足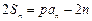 ,
,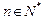 ,其中常数
,其中常数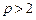 .
.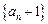 为等比数列;
为等比数列;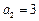 ,求数列
,求数列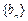 满足
满足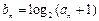 (
(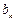 与
与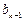 之间插入
之间插入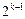 (
(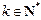 )个2,得到一个新的数列
)个2,得到一个新的数列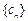 ,试问:是否存在正整数m,使得数列
,试问:是否存在正整数m,使得数列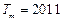 ?如果存在,求出m的值;如果不存在,说明理由.
?如果存在,求出m的值;如果不存在,说明理由. (本小题满分13分)
(本小题满分13分) 中,
中, 已知
已知 ,
, .
. ,求数列
,求数列 的前
的前
 项和
项和 .
. 是等差数列,
是等差数列, ,则该数列前13项和
,则该数列前13项和 等于
等于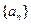 前n项和为
前n项和为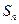 。若
。若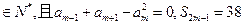 ,则m等于
,则m等于