Question

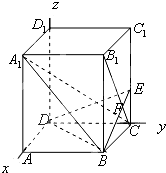已知正四棱柱ABCD-A₁B₁C₁D₁中，底面边长AB=2，侧棱BB₁的长为4，过点B作B₁C的垂线交侧棱CC₁于点E，交B₁C于点F．
（1）求异面直线BA₁和D₁B₁所成的角的余弦值；
（2）证明A₁C⊥平面BED；
（3）求平面BDA₁与平面BDE所成的角的余弦值．

Answer 1

分析：以D为原点，DA、DC、DD₁所在直线分别为x、y、z轴建立空间直角坐标系D-xyz．
（1）求出

BA1

=（0，-2，4），

D1B1

=（2，2，0），利用向量的夹角公式，可求异面直线BA₁和D₁B₁所成的角的余弦值；
（2）先求

BE

=（-2，0，1），再证明

A1C

⊥

DB

，

A1C

⊥

BE

，可得A₁C⊥平面BED；
（3）求出平面BDA₁的法向量

m

=(-2，2，1)、平面BDE的一个法向量为

A1C

=（-2，2，-4），利用向量的夹角公式，可求平面BDA₁与平面BDE所成的角的余弦值．

解答：以D为原点，DA、DC、DD₁所在直线分别为x、y、z轴建立空间直角坐标系D-xyz，如图，D（0，0，0），A（2，0，0），B（2，2，0），C（0，2，0），A₁（2，0，4），B₁（2，2，4），C₁（0，2，4），D₁（0，0，4）
（1）解：

BA1

=（0，-2，4），

D1B1

=（2，2，0），∴|cos＜

BA1

，

D1B1

＞|=|

BA1 • D1B1

| BA1 || D1B1 |

|=|

-4

2 5 ×2 2

|=

10

10

；
（2）证明：设E（0，2，t），则

BE

=（-2，0，t），

B1C

=（-2，0，-4）．
∵BE⊥B₁C，∴

BE

•

B1C

=0
∴4+0-4t=0，∴t=1．
∴E（0，2，1），∴

BE

=（-2，0，1），
∵

A1C

=（-2，2，-4），

DB

=（2，2，0），
∴

A1C

•

DB

=0，

A1C

•

BE

=0
∴

A1C

⊥

DB

，

A1C

⊥

BE

∵DB∩BE=B，∴A₁C⊥平面BED；
（3）解：

BA1

=（0，-2，4），

DB

=（2，2，0）
设平面BDA₁的法向量为

m

=(x，y，z)，则

-2y+4z=0 2x+2y=0

，∴

m

=(-2，2，1)
由（2）知平面BDE的一个法向量为

A1C

=（-2，2，-4），
∴cos＜

A1C

，

m

＞=

A1C • m

|A1C || m |

=

-4

3×2 6

=-

6

9

∵平面BDA₁与平面BDE所成的角为锐二面角
∴平面BDA₁与平面BDE所成的角的余弦值为

6

9

．

点评：本题考查线面垂直，考查线线角，考查线面角，考查利用空间向量解决立体几何问题，属于中档题．