Question

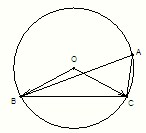（2010•龙岩二模）已知△ABC中，角A、B、C的对边分别为a、b、c，角A不是最大角，a=2

3

，外接圆的圆心为O，半径为2．
（Ⅰ）求

OB

•

OC

的值；
（Ⅱ）若S△ABC=

3

，求△ABC的周长．

Answer 1

分析：（Ⅰ）由三角形ABC的外接圆半径及a的值，利用正弦定理求出sinA的值，再根据A不是最大角，利用特殊角的三角函数值求出A的度数，根据同弧所对的圆心角等于所对圆周角的2倍，由A的度数求出∠BOC的度数，把所求式子利用平面向量的数量积运算法则化简后，将各种的值代入即可求出值；
（Ⅱ）利用三角形的面积公式表示出三角形ABC的面积，把sinA的值代入求出bc的值，然后再利用余弦定理得a²=b²+c²-2bccosA，把a和cosA的值代入，并利用完全平方公式变形后，将bc的值代入求出b+c的值，由a+b+c即可求出三角形的周长．

解答：解：（Ⅰ）∵a=2

3

，R=2，
∴根据正弦定理得：

a

sinA

=2R，即sinA=

a

2R

=

3

2

，
∴∠A=60°或120°，
又∠A不是最大角，
∴0＜∠A＜90°，
∴∠A=60°，
∴∠BOC=120°，又|

OB

|=|

OC

|=2，
则

OB

•

OC

=|

OB

|•|

OC

|cos∠BOC=2×2×（-

1

2

）=-2；
（Ⅱ）∵S_△ABC=

3

，sinA=

3

2

，
∴S_△ABC=

1

2

bcsinA=

1

2

bc•

3

2

=

3

，即bc=4，
∵a=2

3

，cosA=

1

2

，
∴由余弦定理a²=b²+c²-2bccosA得：b²+c²-bc=12，即（b+c）²-3bc=12，
把bc=4代入得：（b+c）²=3bc+12=24，
∴b+c=2

6

，
则△ABC的周长l=a+b+c=2

3

+2

6

．

点评：此题考查了正弦定理，平面向量的数量积运算，圆周角定理，三角形的面积公式，余弦定理，以及完全平方公式的应用，熟练掌握定理及公式是解本题的关键．