题目内容
(2010•龙岩二模)已知a为实数,x=1是函数f(x)=
x2-6x+alnx的一个极值点.
(Ⅰ)求a的值;
(Ⅱ)若函数f(x)在区间(2m-1,m+1)上单调递减,求实数m的取值范围;
(Ⅲ)设函数g(x)=x+
,对于任意x≠0和x1,x2∈[1,5],有不等式|λg(x)|-5ln5≥|f(x1)-f(x2)|恒成立,求实数λ的取值范围.
| 1 |
| 2 |
(Ⅰ)求a的值;
(Ⅱ)若函数f(x)在区间(2m-1,m+1)上单调递减,求实数m的取值范围;
(Ⅲ)设函数g(x)=x+
| 1 |
| x |
分析:(I)利用1处的导数值为0就可求的a的值;
(Ⅱ)利用导数小于0求出函数的递减区间,然后让区间(2m-1,m+1)是求出减区间子区间就可求出参数m的取值范围,还要注意:2m-1<m+1;
(Ⅲ)先利用导数求出函数的极大值和极小值,极大值和极小值之差就是|f(x1)-f(x2)|的最大值,然后让|λg(x)|-5ln5大于等于这个最大值,再用基本不等式求出|λg(x)|
的最小值,便可求出实数λ的取值范围.
(Ⅱ)利用导数小于0求出函数的递减区间,然后让区间(2m-1,m+1)是求出减区间子区间就可求出参数m的取值范围,还要注意:2m-1<m+1;
(Ⅲ)先利用导数求出函数的极大值和极小值,极大值和极小值之差就是|f(x1)-f(x2)|的最大值,然后让|λg(x)|-5ln5大于等于这个最大值,再用基本不等式求出|λg(x)|
的最小值,便可求出实数λ的取值范围.
解答:解:f′(x)=x-6+
(I)f′(1)=0⇒1-6+a=0⇒a=5
(Ⅱ)首先x>0,由(I)得f′(x)=x-6+
=
=
令f′(x)<0,得:1<x<5即f(x)的单调递减区间是(1,5)
∵f(x)在区间(2m-1,m-1)上单调递减
∴(2m-1,m-1)⊆(1,5)⇒
⇒1≤m<2
(Ⅲ)由(I),f(x)=
x2-6x+5lnx,列表如下:
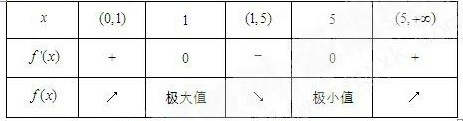
则f(x)极大值=f(1)=-
,f(x)极小值=f(5)=-
+5ln5
∴|f(x1)-f(x2)|≤-
-(-
+5ln5)=12-5ln5
∴|λg(x)|-5ln5≥|f(x1)-f(x2)|恒成立?∴|λg(x)|≥12恒成立
∵|g(x)|=|x+
|=|x|+|
|≥2当且仅当x=±1取等号
|λg(x)|min=|2λ|≥12⇒|λ|≥6⇒λ≤-6或λ≥6
| a |
| x |
(I)f′(1)=0⇒1-6+a=0⇒a=5
(Ⅱ)首先x>0,由(I)得f′(x)=x-6+
| 5 |
| x |
| x2-6x+5 |
| x |
| (x-1)(x-5) |
| x |
令f′(x)<0,得:1<x<5即f(x)的单调递减区间是(1,5)
∵f(x)在区间(2m-1,m-1)上单调递减
∴(2m-1,m-1)⊆(1,5)⇒
|
(Ⅲ)由(I),f(x)=
| 1 |
| 2 |

则f(x)极大值=f(1)=-
| 11 |
| 12 |
| 35 |
| 2 |
∴|f(x1)-f(x2)|≤-
| 11 |
| 2 |
| 35 |
| 2 |
∴|λg(x)|-5ln5≥|f(x1)-f(x2)|恒成立?∴|λg(x)|≥12恒成立
∵|g(x)|=|x+
| 1 |
| x |
| 1 |
| x |
|λg(x)|min=|2λ|≥12⇒|λ|≥6⇒λ≤-6或λ≥6
点评:本题主要考查了利用导数求单调区间及极值的方法,还涉及到恒成立问题转化为求最值问题的一般数学思想,在第2问很容易忽略区间的左端点要小于右端点这一条件,所以本题也属于易错题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目