题目内容
15.已知f(x)为R上的奇函数,当x>0时,f(x)=x2+2x+8,则f(x)的解析式为$f(x)=\left\{\begin{array}{l}-{x^2}+2x-8,x<0\\ 0,x=0\\{x^2}+2x+8,x>0\end{array}\right.$.分析 由奇函数的性质易得f(0)=0,由题意和函数的奇偶性可得当x<0时的解析式,综合可得答案.
解答 解:∵f(x)为R上的奇函数,∴f(0)=0,
设x<0,则-x>0,
∵当x>0时,f(x)=x2+2x+8,
∴f(-x)=(-x)2+2(-x)+8=x2-2x+8,
∴-f(x)=x2-2x+8,
∴当x<0时,f(x)=-x2+2x-8
综上可得f(x)的解析式为:$f(x)=\left\{\begin{array}{l}-{x^2}+2x-8,x<0\\ 0,x=0\\{x^2}+2x+8,x>0\end{array}\right.$
故答案为:$f(x)=\left\{\begin{array}{l}-{x^2}+2x-8,x<0\\ 0,x=0\\{x^2}+2x+8,x>0\end{array}\right.$
点评 本题考查函数解析式的求解,涉及函数的奇偶性和整体的思想,属基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
10.等边三角形ABC的边长是a,AD是BC边上的高,沿AD将△ABC折成直二面角,则点B、C的距离是( )
| A. | $\frac{1}{2}$a | B. | $\frac{\sqrt{2}}{2}$a | C. | $\frac{\sqrt{3}}{2}$a | D. | a |
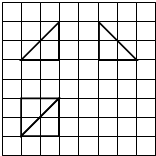 如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱与底面所成角的正弦值为$\frac{\sqrt{3}}{3}$.
如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱与底面所成角的正弦值为$\frac{\sqrt{3}}{3}$.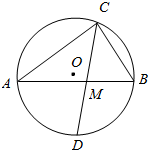 如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.
如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.