题目内容
设函数f(x)＝
cos2ωx＋sinωxcosωx＋a(其中ω＞0，a∈R)，且f(x)的图象在y轴右侧的第一个最高点的横坐标是
．
(1)求ω的值；
(2)如果f(x)在区间[－
，
]上的最小值为，求a的值．
答案：
解析：
解析：
|
思路分析：利用两角和差三角公式将函数的解析式化为y＝Asin(ωx＋ 解：(1)f(x)＝ 依题意得2ω· 解得ω＝ (2)由(1)，知f(x)＝sin(x＋ 又当x∈[－ 从而f(x)在[－ 因此，由题设知－ 故a＝ |
)＋B(A＞0，ω＞0)的形式，再利用它的性质求解．
cos2ωx＋
sin2ωx＋
)＋
＋
，
]时，x＋
]，故－
．
练习册系列答案
相关题目
cos2ωx＋sinωxcosωx＋a(其中ω＞0，a∈R)，且f(x)的图象在y轴右侧的第一个最高点的横坐标为
．
，
]上的最小值为
cos2ωx＋sinωxcosωx＋a(其中ω＞0，a∈R)且f(x)的图象在y轴右侧的第一个最高点的横坐标为
．
上的最小值为
，求a的值．
)，g(x)＝1＋
sin2x．
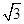cos2ωx＋sinωxcosωx＋a(其中ω>0，a∈R)，且f(x)的图象在y轴右侧的第一个最高点的横坐标为
.
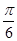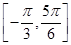上的最小值为