题目内容
设函数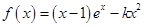 (其中
(其中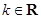 ).
).
(1) 当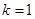 时,求函数
时,求函数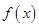 的单调区间;
的单调区间;
(2) 当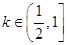 时,求函数
时,求函数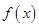 在
在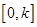 上的最大值
上的最大值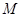 .
.
(1) 函数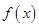 的递减区间为
的递减区间为 ,递增区间为
,递增区间为 ,
, ;
;
(2) 
解析试题分析:(1)由
 ,利用导数的符号判断函数
,利用导数的符号判断函数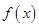 的单调性和求单调区间;
的单调性和求单调区间;
(2)
试题解析:
解:(1)当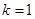 时,
时, ,
,
令 ,得
,得 ,
,
当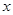 变化时,
变化时, 的变化如下表:
的变化如下表: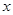











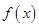
单调递增 极大值 单调递减 极小值 单调递增
右表可知,函数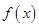 的递减区间为
的递减区间为 ,递增区间为
,递增区间为 ,
, .
.
(2)  ,令
,令 ,得
,得 ,
, , 令
, 令 ,则
,则
练习册系列答案
相关题目
 。
。 与
与 在公共点
在公共点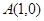 处有相同的切线,求实数
处有相同的切线,求实数 的值;
的值;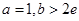 ,求方程
,求方程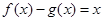 在区间
在区间 内实根的个数(
内实根的个数( 为自然对数的底数).
为自然对数的底数).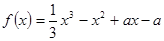 (
(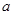
 R).
R).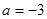 时,求函数
时,求函数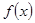 的极值;
的极值;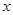 轴有且只有一个交点,求
轴有且只有一个交点,求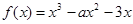 ,
,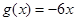 (
(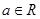 ).
).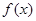 的极值点,求
的极值点,求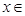 [1,a]上的最小值和最大值;
[1,a]上的最小值和最大值;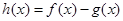 在
在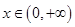 时是增函数,求实数a的取值范围.
时是增函数,求实数a的取值范围.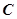 (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积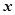 (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是 为常数).记
为常数).记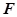 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.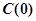 的实际意义,并建立
的实际意义,并建立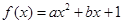 在
在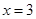 处的切线方程为
处的切线方程为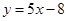 .
. 的解析式;
的解析式;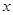 的方程
的方程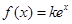 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数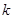 的值;
的值;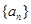 满足
满足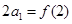 ,
,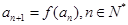 ,求
,求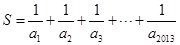 的整数部分.
的整数部分. .
. 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和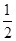 x2+2x+kln x,其中k≠0.
x2+2x+kln x,其中k≠0.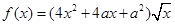 ,其中
,其中 .
. 时,求
时,求 的单调递增区间;
的单调递增区间;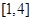 上的最小值为8,求
上的最小值为8,求 的值.
的值.