题目内容
在等比数列中,若a2=2,a6=162,求a10.
思路解析一:把已知条件都用a1,q来表示,转化为关于a1,q的方程组,求出a1和q,用通项公式可以求出该等比数列中的任何一项. 解法一:设等比数列的首项为a1,公比为q,根据题意, 有 ∴ ∴a10=a1q9=13 122. 思路解析二:已知等比数列中的任何两项,用an=am·qn-m也可求出等比数列中的任何一项. 解法二:∵a6=a2q4,其中a2=2,a6=162, ∴q4=81. ∴a10=a6·q4=162×81=13 122. 思路解析三:利用结论“若三数m,n,p成等差数列,则等比数列{an}中的am,an,ap三项成等比(m,n,p∈N*)”求解. 解法三:根据等比数列的性质,a2,a6,a10成等比数列, ∴a62=a2·a10.∴a10= 思路解析四:利用“在等比数列中,若m+n=p+q,m,n,p,q∈N*,则aman=apaq”求解. 解法四:∵2+10=6+6=12,∴在等比数列中,有a2·a10=a6·a6=a62, ∴a10=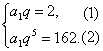
![]() ,得q4=81.
,得q4=81.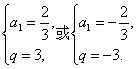
![]() =
=![]() =162×81=13 122.
=162×81=13 122.![]() =13 122.
=13 122.
快乐口算系列答案
决胜百分百系列答案
小升初真题精选系列答案
基础天天练系列答案
夺冠训练归类模拟总复习系列答案
天府优学系列答案
小升初模拟冲刺卷系列答案
新考题大集结系列答案
中学英语听读导航系列答案
同步宝典1线超越系列答案