题目内容
设 其中
其中 .
.(1)求
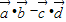 的取值范围;
的取值范围;(2)若
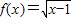 ,
,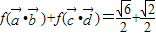 ,求cosθ-sinθ的值.
,求cosθ-sinθ的值.
【答案】分析:利用向量的数量积的坐标表示求出 ①
①
(1)利用二倍角公式化简①,由已知 结合三角函数的图象可求取值范围.
结合三角函数的图象可求取值范围.
(2)由已知整理可得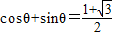 ⇒
⇒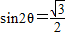 ,结合题中
,结合题中 可求θ,从而可得结果.
可求θ,从而可得结果.
(法二)由 可得sinθ>cosθ,要求cosθ-sinθ,可先求(cosθ-sinθ)2
可得sinθ>cosθ,要求cosθ-sinθ,可先求(cosθ-sinθ)2
解答:解: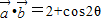
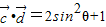 (2分)
(2分)
(1) (4分)
(4分)
∵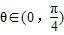
∴2cos2θ∈(0,2)
即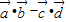 的取值范围是(0,2)(7分)
的取值范围是(0,2)(7分)
(2)∵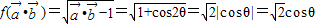
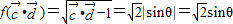 (10分)
(10分)
∴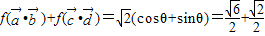
∴
∴
∴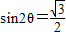
因为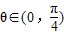 所以
所以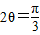
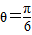
故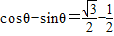 (14分)
(14分)
(注亦可:
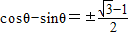
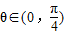
sinθ<cosθ∴ )
)
点评:本题以平面向量数量积的坐标表示为载体,综合考查了向量数量积的运算,同角平方关系,二倍角公式,平面向量与三角函数的综合考查一直是进几年高考的重点内容之一,要重点掌握.
 ①
①(1)利用二倍角公式化简①,由已知
 结合三角函数的图象可求取值范围.
结合三角函数的图象可求取值范围.(2)由已知整理可得
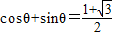 ⇒
⇒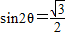 ,结合题中
,结合题中 可求θ,从而可得结果.
可求θ,从而可得结果.(法二)由
 可得sinθ>cosθ,要求cosθ-sinθ,可先求(cosθ-sinθ)2
可得sinθ>cosθ,要求cosθ-sinθ,可先求(cosθ-sinθ)2解答:解:
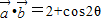
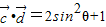 (2分)
(2分)(1)
 (4分)
(4分)∵
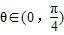
∴2cos2θ∈(0,2)
即
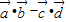 的取值范围是(0,2)(7分)
的取值范围是(0,2)(7分)(2)∵
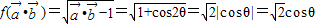
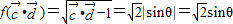 (10分)
(10分)∴
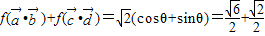
∴

∴

∴
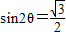
因为
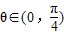 所以
所以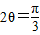
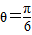
故
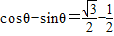 (14分)
(14分)(注亦可:

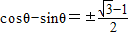
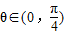
sinθ<cosθ∴
 )
)点评:本题以平面向量数量积的坐标表示为载体,综合考查了向量数量积的运算,同角平方关系,二倍角公式,平面向量与三角函数的综合考查一直是进几年高考的重点内容之一,要重点掌握.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 =(1,cos2θ),
=(1,cos2θ), =(2,1),
=(2,1),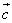 =(4sinθ,1),
=(4sinθ,1),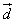 =(
=(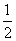 sinθ,1),其中
sinθ,1),其中 。
。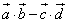 的取值范围;
的取值范围;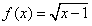 ,
,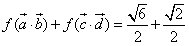 ,求cosθ-sinθ的值.
,求cosθ-sinθ的值. 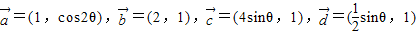 其中
其中 .
.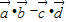 的取值范围;
的取值范围; ,
,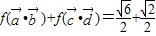 ,求cosθ-sinθ的值.
,求cosθ-sinθ的值. 其中
其中 .
. 的取值范围;
的取值范围; ,
, ,求cosθ-sinθ的值.
,求cosθ-sinθ的值.