题目内容
12.设0<a<1,实数x,y满足$|x|-{log_a}\frac{1}{y}=0$,则y关于x的函数的图象形状大致是( )| A. | 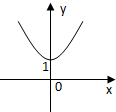 | B. | 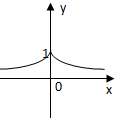 | C. |  | D. | 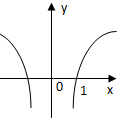 |
分析 函数y=$\frac{1}{{a}^{|x|}}$,显然y在(0,+∞)上单调递增,且函数的图象经过点(0,1),从而得出结论.
解答 解:0<a<1,实数x,y满足$|x|-{log_a}\frac{1}{y}=0$,即y=$\frac{1}{{a}^{|x|}}$,故函数y为偶函数,它的图象关于y轴对称,
在(0,+∞)上单调递增,且函数的图象经过点(0,1),
故选:A.
点评 本题主要指数式与对数式的互化,函数的奇偶性、单调性以及特殊点,属于中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
4.已知实数x,y满足x2+y2-4x+2=0,则x2+(y-2)2的最小值是( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | 8 |
1.600°角是第( )象限的角.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
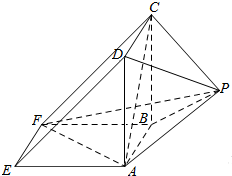 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.