题目内容
15. 如图,某动物种群数量1月1日低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.
如图,某动物种群数量1月1日低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.(1)求出种群数量y关于时间t的函数表达式;(其中t以年初以来的月为计量单位)
(2)估计当年3月1日动物种群数量.
分析 (1)由题意,设y=100sin(ωt+θ)+800,利用周期求出ω,(6,900)代入可得θ,即可求出种群数量y关于时间t的函数表达式;
(2)t=3代入,估计当年3月1日动物种群数量.
解答 解:(1)由题意,设y=100sin(ωt+θ)+800,
$\frac{T}{2}$=6,∴T=12=$\frac{2π}{ω}$,
∴ω=$\frac{π}{6}$,
∴y=100sin($\frac{π}{6}$t+θ)+800,
(6,900)代入可得900=100sin($\frac{π}{6}$×6+θ)+800,
∴θ=-$\frac{π}{2}$,
∴y=100sin($\frac{π}{6}$t-$\frac{π}{2}$)+800=-100cos$\frac{π}{6}$t+800;
(2)t=3,y=-100cos$\frac{π}{2}$+800=800.
点评 本题考查三角函数模型的运用,考查学生利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.设正项等差数列{an}的前n项和为Sn,已知S5=40,且a4,a8-1,a15成等比数列,则S15等于( )
| A. | 225 | B. | 345 | C. | 350 | D. | 535 |
6.已知幂函数f(x)=(m-1)xa的图象过点(9,3),数列{an}各项均为正值,且a1=$\frac{m}{2}$,a2=m,且$\frac{{a}_{n}}{{a}_{n-1}}$=f($\frac{{a}_{n+1}}{{a}_{n}}$)(n>1),则a10=( )
| A. | 210 | B. | 245 | C. | 288 | D. | 2511 |
4.已知函数f(x)=sinωxcosωx在区间[-$\frac{π}{6}$,$\frac{π}{3}$]上单调递增,则正数ω的最大值是( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为3的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为3的等腰三角形. 已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.
已知圆O:x2+y2=4和圆C:x2+y2-2x-y-2=0,记两圆的公共弦所在的直线为l.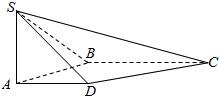 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2. 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别是A1D1,A1A的中点.