题目内容
7.已知数列{an}为等差数列,a2=5,a4=11,数列{bn}是等比数列,b1=1,b4=64.(1)分别求{an}和{bn}的通项公式;
(2)设Tn=a1b1+a2b2+…+anbn,求Tn.
分析 (1)通过a2=5、a4=11可得公差,进而可得通项公式;通过b1=1、b4=64可得公比,进而可得通项公式;
(2)通过an=3n-1、bn=4n-1可得Tn、4Tn的表达式,利用错位相减法及等比数列的求和公式计算可得结论.
解答 解:(1)∵数列{an}为等差数列,a2=5,a4=11,
∴数列{an}的公差d=$\frac{{a}_{4}-{a}_{2}}{2}$=$\frac{11-5}{2}$=3,
∴a1=a2-d=5-3=2,
∴an=2+3(n-1)=3n-1;
∵数列{bn}是等比数列,b1=1,b4=64,
∴数列{bn}的公比q=$\root{3}{\frac{{b}_{4}}{{b}_{1}}}$=$\root{3}{\frac{64}{1}}$=4,
∴bn=b1•qn-1=4n-1;
(2)∵an=3n-1,bn=4n-1,
∴anbn=(3n-1)4n-1,
∴Tn=a1b1+a2b2+…+anbn
=2×1+5×4+8×42+…+(3n-4)4n-2+(3n-1)4n-1,
∴4Tn=2×4+5×42+…+(3n-4)4n-1+(3n-1)4n,
两式相减得:-3Tn=2+3×4+3×42+…+3×4n-1-(3n-1)4n
=2+3(4+42+…+4n-1)-(3n-1)4n
=2+3×$\frac{4(1-{4}^{n-1})}{1-4}$-(3n-1)4n
=(2-3n)4n-2,
∴Tn=$\frac{(2-3n)•{4}^{n}-2}{-3}$=n•4n+$\frac{2}{3}$•(1-4n).
点评 本题考查求数列的通项公式,考查错位相减法,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.已知x1、x2是函数f(x)=|lnx|-e-x的两个零点,则x1x2所在区间是( )
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
19.已知ω>0,0<φ<π,点A($\frac{π}{4}$,0)和点B($\frac{5π}{4}$,0)是函数f(x)=sin(ωx+φ)的图象的两个相邻的对称中心,则φ=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
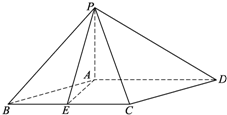 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.