题目内容
12.已知x1、x2是函数f(x)=|lnx|-e-x的两个零点,则x1x2所在区间是( )| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1) | C. | (1,2) | D. | (2,e) |
分析 能够分析出f(x)的零点便是函数|lnx|和函数e-x交点的横坐标,从而可画出这两个函数图象,由图象可看出$\left\{\begin{array}{l}{0<-ln{x}_{1}<1}\\{0<ln{x}_{2}<1}\\{-ln{x}_{1}>ln{x}_{2}}\end{array}\right.$,这样即可得出-1<lnx1x2<0,根据对数函数的单调性即可求出$\frac{1}{e}<{x}_{1}{x}_{2}<1$.
解答 解:令f(x)=0,∴|lnx|=e-x;
∴函数f(x)的零点便是上面方程的解,即是函数|lnx|和函数e-x的交点,画出这两个函数图象如下: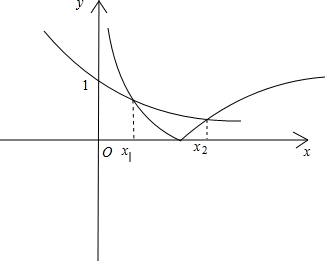 由图看出0<-lnx1<1,-1<lnx1<0,0<lnx2<1;
由图看出0<-lnx1<1,-1<lnx1<0,0<lnx2<1;
∴-1<lnx1+lnx2<1;
∴-1<lnx1x2<1;
∴$\frac{1}{e}<{x}_{1}{x}_{2}<e$;
由图还可看出,-lnx1>lnx2;
∴lnx1x2<0,x1x2<1;
∴x1x2的范围是($\frac{1}{e},1$).
故选B.
点评 考查函数零点的概念,函数零点和方程解的关系,方程f(x)=g(x)的解和函数f(x)与g(x)交点的关系,对数的运算,以及对数函数的单调性.

练习册系列答案
相关题目
3.已知等差数列{an}的公差d≠0,若a1,a3,a9成等比数列,那么公比为( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | 2 |
17.已知变量x、y满足约束条件:$\left\{\begin{array}{l}{y≥x}\\{x+2y≤2}\\{x≥-2}\end{array}\right.$,则z=x-3y的最小值是( )
| A. | -$\frac{4}{3}$ | B. | 4 | C. | -4 | D. | -8 |