题目内容
17.函数y=tanx(-$\frac{π}{4}$≤x≤$\frac{π}{4}$,且x≠0)的值域是[-1,0)∪(0,1].分析 根据正切函数的单调性进行求解即可.
解答 解:∵-$\frac{π}{4}$≤x≤$\frac{π}{4}$,且x≠0,
∴在-$\frac{π}{4}$≤x<0,0<x≤$\frac{π}{4}$上,y=tanx为增函数,
则tan(-$\frac{π}{4}$)≤tanx<0或0<tanx≤tan$\frac{π}{4}$,
即-1≤tanx<0或0<tanx≤1,
即函数的值域为[-1,0)∪(0,1],
故答案为:[-1,0)∪(0,1]
点评 本题主要考查三角函数的值域的求解,利用正切函数的单调性是解决本题的关键.

练习册系列答案
相关题目
8.已知全集U=R,A={x|x<1},B={x|x≥2},则集合∁U(A∪B)=( )
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
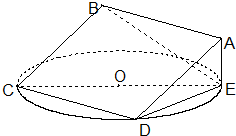 如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.
如图,正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面.