题目内容
(本小题共14分)
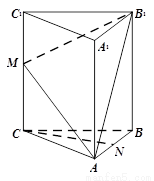
如图,在四棱锥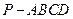 中,
中,
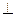 平面
平面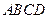 ,底面
,底面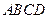 是菱形,
是菱形,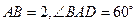 .
.
(Ⅰ)求证: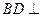 平面
平面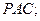
(Ⅱ)若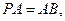 求
求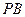 与
与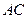 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面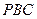 与平面
与平面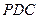 垂直时,求
垂直时,求 的长.
的长.
:证明:(Ⅰ)因为四边形ABCD是菱形,所以 又因为
又因为 平面
平面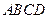 。所以
。所以 ,
,
所以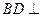 平面
平面 。
。
(Ⅱ) 设
设 ,因为
,因为
所以 ,如图,以O为坐标原点,建立空间直角坐标系
,如图,以O为坐标原点,建立空间直角坐标系 ,则
,则 所
所 设
设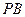 与
与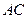 所成角为
所成角为 ,则
,则

(Ⅲ)由(Ⅱ)知 设
设
 。则
。则 设平面
设平面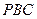 的法
的法
向量 则
则 ,所以
,所以 令
令 则
则
 ,
,
所以 同理,平面
同理,平面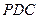 的法向量
的法向量
 ,因为平面
,因为平面
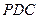 ,所以
,所以 ,即
,即 解得
解得 ,所以
,所以

解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


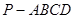 中,底面
中,底面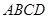 为平行四边形,
为平行四边形,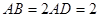 ,
,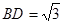 ,
, ⊥底面
⊥底面
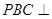 平面
平面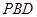 ;
;
 为
为 ,求
,求 与平面
与平面 所成角的正弦值。
所成角的正弦值。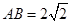 ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.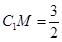 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.