题目内容
8.已知圆O:x2+y2=1和动点P(m,-2),圆C是以OP为直径的圆,圆O与圆C相交,设交点为A,B.(1)问直线AB是否过定点?若过定点,请求出定点坐标;若不过定点,请说明理由;
(2)记直线OA,OB,AB的斜率分别为k1,k2,k,若k1+1,k,k2+1依次成等差数列,求直线AB的方程.
分析 (1)设出直线AB的方程代入x2+y2=1,圆C:(x-$\frac{m}{2}$)2+(y+1)2=$\frac{{m}^{2}+4}{4}$,可得b-1=b2+2b,求出b,即可得出结论;
(2)利用等差数列的性质,求出m,即可求直线AB的方程.
解答 解:(1)设直线AB的方程为y=kx+b,
∵kPO=-$\frac{2}{m}$,∴kAB=$\frac{m}{2}$,
∴y=$\frac{m}{2}$x+b,
代入x2+y2=1,圆C:(x-$\frac{m}{2}$)2+(y+1)2=$\frac{{m}^{2}+4}{4}$,
可得$\frac{{m}^{2}+4}{4}$x2+mbx+b-1=0与$\frac{{m}^{2}+4}{4}$x2+mbx+b2+2b=0,
∴b-1=b2+2b,
∴b=-$\frac{1}{2}$,
∴y=$\frac{m}{2}$x-$\frac{1}{2}$,
∴直线l过定点(0,-$\frac{1}{2}$);
(2)$\frac{{m}^{2}+4}{4}$x2+mbx+b-1=0为$\frac{{m}^{2}+4}{4}$x2-$\frac{1}{2}$mx-$\frac{3}{4}$=0
∴(4+m2)x2-2mx-3=0,
∴k1=$\frac{{y}_{1}}{{x}_{1}}$=$\frac{\frac{m}{2}{x}_{1}-\frac{1}{2}}{{x}_{1}}$,k=$\frac{m}{2}$,k2=$\frac{\frac{m}{2}{x}_{2}-\frac{1}{2}}{{x}_{2}}$,
∵k1+1,k,k2+1依次成等差数列,
∴2k=k1+1+k2+1,
代入整理可得m-2=m-$\frac{{x}_{1}+{x}_{2}}{2{x}_{1}{x}_{2}}$,
∴-2=$\frac{m}{3}$,
∴m=-6,
∴y=-3x-$\frac{1}{2}$.
点评 本题考查了直线与圆锥曲线的位置关系,考查了等差数列的应用,训练了数学转化思想方法,属于中档题.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
| A. | 8 | B. | 12 | C. | 16 | D. | 24 |
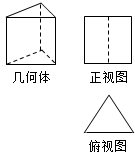 如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为4,且侧棱垂直于底面,正视图是边长为4的正方形,则三棱柱的左视图面积为( )| A. | 8$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 4$\sqrt{3}$ |
| t | 1.99 | 3.0 | 4.0 | 5.1 | 6.12 |
| y | 1.50 | 4.04 | 7.50 | 12.00 | 18.01 |
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是④(填序号).
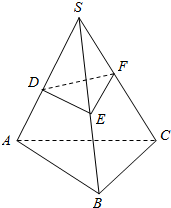 如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.
如图.D、E、F分别是三棱锥S-ABC,侧棱SA、SB、SC上的点.且SD:DA=SE:EB=CF:FS=2:1.那么过D、E、F的 平面截三棱锥S-ABC所得上下两部分体积的比为4:23.