题目内容
已知O是坐标原点,点A(-1,-2),若点M(x,y)平面区域
上的一个动点,使
•(
-
)+
≤0恒成立,则实数m的取值范围为______.
|
| OA |
| OA |
| MA |
| 1 |
| m |
不等式组表示的平面区域如图

令z=
•(
-
)=
•
=-x-2y,则目标函数的几何意义是直线y=-
x-
纵截距一半的相反数
由
,可得x=y=1由图象可知,此时z取得最大值-3
∵
•(
-
)+
≤0恒成立
∴
≤-
•(
-
)+
∴
≤-z
∴
≤3
∴m<0或m≥
故答案为:(-∞,0)∪[
,+∞).

令z=
| OA |
| OA |
| MA |
| OA |
| OM |
| 1 |
| 2 |
| z |
| 2 |
由
|
∵
| OA |
| OA |
| MA |
| 1 |
| m |
∴
| 1 |
| m |
| OA |
| OA |
| MA |
| 1 |
| m |
∴
| 1 |
| m |
∴
| 1 |
| m |
∴m<0或m≥
| 1 |
| 3 |
故答案为:(-∞,0)∪[
| 1 |
| 3 |

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
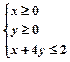 所确定的平面区域内,则点B(m-n,m+n)所在平面区域的面积为( )
所确定的平面区域内,则点B(m-n,m+n)所在平面区域的面积为( ) 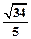
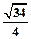
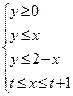 所确定的区域面积为S,记
所确定的区域面积为S,记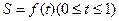 ,则
,则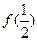 =▲
=▲
