题目内容
已知平面向量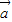 ,
,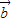 满足
满足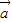 •(
•(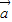 +
+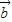 )=3,且|
)=3,且|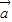 |=2,|
|=2,|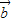 |=1,则向量
|=1,则向量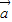 与
与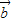 的夹角为( )
的夹角为( )A.
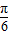
B.
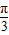
C.
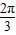
D.
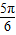
【答案】分析:根据向量数量积的性质,得到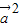 =
=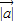 2=4,代入已知等式得
2=4,代入已知等式得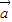 •
•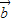 =-1.设
=-1.设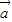 与
与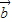 的夹角为α,结合向量数量积的定义和
的夹角为α,结合向量数量积的定义和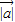 =2,
=2,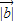 =1,算出cosα=-
=1,算出cosα=- ,最后根据两个向量夹角的范围,可得
,最后根据两个向量夹角的范围,可得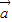 与
与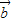 夹角的大小.
夹角的大小.
解答:解:∵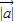 =2,∴
=2,∴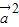 =4
=4
又∵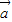 •(
•(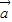 +
+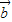 )=3,
)=3,
∴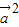 +
+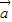 •
•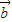 =4+
=4+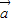 •
•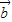 =3,得
=3,得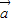 •
•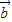 =-1,
=-1,
设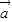 与
与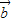 的夹角为α,
的夹角为α,
则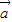 •
•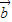 =
=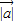
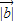 cosα=-1,即2×1×cosα=-1,得cosα=-
cosα=-1,即2×1×cosα=-1,得cosα=-
∵α∈[0,π],
∴α=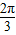
故选C
点评:本题给出两个向量的模,并且在已知它们的和向量与其中一个向量数量积的情况下,求两个向量的夹角.着重考查了平面向量数量积的运算和两个向量夹角等知识,属于基础题.
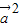 =
=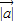 2=4,代入已知等式得
2=4,代入已知等式得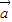 •
•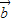 =-1.设
=-1.设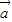 与
与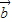 的夹角为α,结合向量数量积的定义和
的夹角为α,结合向量数量积的定义和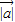 =2,
=2,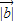 =1,算出cosα=-
=1,算出cosα=- ,最后根据两个向量夹角的范围,可得
,最后根据两个向量夹角的范围,可得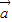 与
与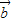 夹角的大小.
夹角的大小.解答:解:∵
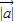 =2,∴
=2,∴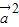 =4
=4又∵
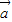 •(
•(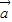 +
+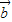 )=3,
)=3,∴
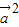 +
+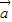 •
•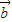 =4+
=4+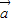 •
•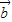 =3,得
=3,得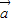 •
•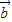 =-1,
=-1,设
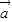 与
与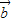 的夹角为α,
的夹角为α,则
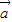 •
•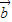 =
=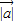
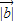 cosα=-1,即2×1×cosα=-1,得cosα=-
cosα=-1,即2×1×cosα=-1,得cosα=-
∵α∈[0,π],
∴α=
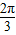
故选C
点评:本题给出两个向量的模,并且在已知它们的和向量与其中一个向量数量积的情况下,求两个向量的夹角.着重考查了平面向量数量积的运算和两个向量夹角等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 满足:
满足: ,则
,则 的夹角为
的夹角为  ,且α与
,且α与 的夹角为
的夹角为 ,则
,则 的取值范围是
;
的取值范围是
; ,满足
,满足 。若
。若
 有最大值
有最大值 B.
B. D.
D.