题目内容
已知某工厂生产x件产品的成本为c=25 000+200x+
x2(元). (1)要使平均成本最低,应生产多少件产品?
(2)若产品以每件500元售出,要使利润最大,应生产多少件产品?
思路分析:本题已直接给出了函数关系式,可直接求解.该题不仅可以用导数方法来求,也可以利用重要不等式来解.
解:(1)设平均成本为y元,则y=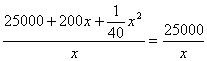+200+
(x＞0).
y′=(
)′=
.
令y′=0,得x1=1 000,x2=-1 000(舍去).
当在x=1 000附近左侧时,y′＜0;当在x=1 000附近右侧时,y′＞0,故当x=1 000时,y取得极小值.由于函数只有一个点使y′=0,且函数在该点有极小值,那么函数在该点取得最小值,因此要使成本最低,应生产1 000件产品.
(2)利润函数L=500x-(25 000+200x+
)=300x-25 000-
.
∴L′=(300x-25 000-
)′=300-
.
令L′=0,得x=6 000,当x在6 000附近左侧时,L′＞0;
当x在6 000附近右侧时,L′＜0,
故当x=6 000时,L取得最大值.
由于函数只有一个使L′=0的点,且函数在该点有极大值,那么函数在该点取得最大值.因此,要使利润最大,应生产6 000件产品.
某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品.
（1）已知甲、乙两种产品每一道工序的加工结
果为A级的概率如表一所示，分别求生产
出的甲、乙产品为一等品的概率P甲、P乙；
（2）已知一件产品的利润如表二所示，用ξ、
η分别表示一件甲、乙产品的利润，在
（I）的条件下，求ξ、η的分布列及
Eξ、Eη；
（3）已知生产一件产品需用的工人数和资金额
如表三所示.该工厂有工人40名，可用资.
|
|
品的数量，在（II）的条件下，x、y为何 值时，
最大？最大值是多少？
（解答时须给出图示）
某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均
为二等品.
（1）已知甲、乙两种产品每一道工序的加工结
果为A级的概率如表一所示，分别求生产
出的甲、乙产品为一等品的概率P甲、P乙；
（2）已知一件产品的利润如表二所示，用ξ、
η分别表示一件甲、乙产品的利润，在
（1）的条件下，求ξ、η的分布列及Eξ、
Eη；
（3）已知生产一件产品需用的工人数和资金额
如表三所示.该工厂有工人40名，可用资.
|
|
品的数量，在（2）的条件下，x、y为何
值时，
最大？最大值是多少？
（解答时须给出图示）