Question

【题目】已知定义域为的函数（，）

（1）设，求的单调区间；

（2）设为导数，

（i）证明：当，时，；

（ii）设关于的方程的根为，求证：

Answer 1

【答案】（1）当为奇数时的增区间为，减区间为；当为偶数时的增区间为及，减区间为。

（2）（i）证明见解析，（ii）证明见解析。

【解析】

（1）对，求导可得，分当为大于1的奇数，和为偶数时两种情况讨论可得的单调区间；

（2）（i）设，，求导得，根据研究即可得到所证结论；

（ii），原方程化为解得，因为，所以；作差得，，由（i）知，可得，所以，即可得证.

（1），

当，时

即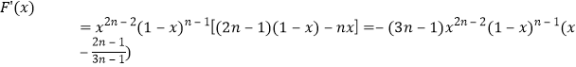

（a）当为大于1的奇数时，是偶数，，，

当时，，当时

故的增区间为，减区间为

当为偶数时，是奇数，由于，所以

当或时，，当时

故的增区间为及，减区间为

综上，当为奇数时的增区间为，减区间为，

当为偶数时的增区间为及，减区间为，

（2）（i）证明：设，，则，

因为，，故在是增函数，

从而，由于，

所以，

所以在是增函数，，即

（ii），原方程化为

解得，因为，所以；

作差得，，

由（i）知，当，时，，

令，，故有，所以，，

综上，