题目内容
在△ABC中,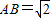 ,BC=1,
,BC=1,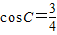 .
.(Ⅰ)求sinA的值;
(Ⅱ)求
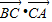 的值.
的值.
【答案】分析:(1)利用同角三角函数基本关系,根据cosC,求得sinC,进而利用正弦定理求得sinA.
(2)先根据余弦定理求得b,进而根据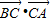 =BC•CA•cos(π-C)求得答案.
=BC•CA•cos(π-C)求得答案.
解答:解:(1)在△ABC中,由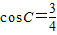 ,得
,得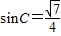 ,
,
又由正弦定理: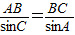 得:
得: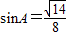 .
.
(2)由余弦定理:AB2=AC2+BC2-2AC•BC•cosC得: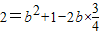 ,
,
即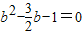 ,解得b=2或
,解得b=2或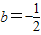 (舍去),所以AC=2.
(舍去),所以AC=2.
所以,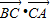 =BC•CA•cos(π-C)=
=BC•CA•cos(π-C)=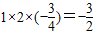
即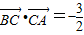 .
.
点评:本题主要考查了正弦定理的应用,平面向量数量积的计算.考查了学生综合运用所学知识的能力.
(2)先根据余弦定理求得b,进而根据
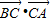 =BC•CA•cos(π-C)求得答案.
=BC•CA•cos(π-C)求得答案.解答:解:(1)在△ABC中,由
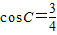 ,得
,得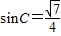 ,
,又由正弦定理:
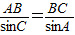 得:
得: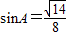 .
.(2)由余弦定理:AB2=AC2+BC2-2AC•BC•cosC得:
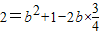 ,
,即
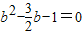 ,解得b=2或
,解得b=2或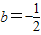 (舍去),所以AC=2.
(舍去),所以AC=2.所以,
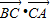 =BC•CA•cos(π-C)=
=BC•CA•cos(π-C)=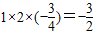
即
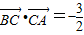 .
.点评:本题主要考查了正弦定理的应用,平面向量数量积的计算.考查了学生综合运用所学知识的能力.

练习册系列答案
相关题目
 如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC′上的高,则
如图,在△ABC中,AB=BC=4,∠ABC=30°,AD是边BC′上的高,则| AD |
| AC |
| A、0 | B、4 | C、8 | D、-4 |
 13、13、如图在△ABC中,AD⊥BC,ED=2AE,过E作FG∥BC,且将△AFG沿FG折起,使∠EA'D=90°,则二面角A'-FG-B的大小为
13、13、如图在△ABC中,AD⊥BC,ED=2AE,过E作FG∥BC,且将△AFG沿FG折起,使∠EA'D=90°,则二面角A'-FG-B的大小为 如图,在△ABC中,
如图,在△ABC中,