题目内容
设f(x)=x2+bx+c,x∈[-1,1],证明当b<-2时,在其定义域范围内至少存在一个x,使|f(x)|≥
证明:假设不存在x∈[-1,1]上满足|f(x)|≥![]() ,
,
则对于x∈[-1,1]上的任意x有-![]() <f(x)<
<f(x)<![]() 成立.?
成立.?
∴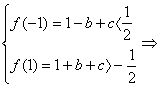 b>-
b>-![]() 与b<-2矛盾.?
与b<-2矛盾.?
故假设不成立,即原命题成立.

练习册系列答案
相关题目
设f(x)=
,g(x)是二次函数,若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
|
| A、(-∞,-1]∪[1,+∞) |
| B、(-∞,-1]∪[0,+∞) |
| C、[0,+∞) |
| D、[1,+∞) |