题目内容
连掷两次骰子得到的点数分别为m和n,向量 =(m,n)和向量
=(m,n)和向量 =(1,-1)的夹角为θ,则θ为锐角的概率是
=(1,-1)的夹角为θ,则θ为锐角的概率是
- A.

- B.

- C.

- D.

D
分析:掷两次骰子分别得到的点数m,n,组成的向量(m,n)个数为36个,只需列举出满足条件的即可.
解答:后连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种
由于向量(m,n)与向量(1,-1)的夹角θ为锐角,∴(m,n)•(1,-1)>0,
即m>n,满足题意的情况如下:
当m=2时,n=1;
当m=3时,n=1,2;
当m=4时,n=1,2,3;
当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5;共有15种,
故所求事件的概率为: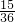 =
= ,
,
故选D
点评:本题考查等可能事件的概率,得出m>n并正确列举是解决问题的关键,属基础题.
分析:掷两次骰子分别得到的点数m,n,组成的向量(m,n)个数为36个,只需列举出满足条件的即可.
解答:后连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种
由于向量(m,n)与向量(1,-1)的夹角θ为锐角,∴(m,n)•(1,-1)>0,
即m>n,满足题意的情况如下:
当m=2时,n=1;
当m=3时,n=1,2;
当m=4时,n=1,2,3;
当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5;共有15种,
故所求事件的概率为:
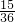 =
= ,
,故选D
点评:本题考查等可能事件的概率,得出m>n并正确列举是解决问题的关键,属基础题.

练习册系列答案
相关题目



