Question

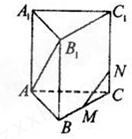
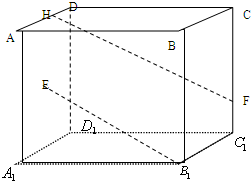
如图，已知正方体ABCD-A₁B₁C₁D₁，棱长为4，E为面A₁D₁DA的中心，
CF=3FC₁，AH=3HD，
（1）求异面直线EB₁与HF之间的距离
（2）求二面角H-B₁E-A₁的平面角的余弦值．

Answer 1

如图建立直角坐标系D₁-xyz，则E（2，0，2），B₁（4，4，0），H（1，0，4）
（1）

EB1

=（2，4，-2），

HF

=（-1，4，-3）

EH

=（-1，0，2），设

n

=（x，y，z）

n • EB1 =0 n • HF =0

即

2x+4y-2z=0 -x+4y-3z=0

，取x=1，则z=-3，y=-2，
则

n

=（1，-2，-3）
异面直线EB₁与HF之间的距离为

| n • EH |

| n |

=

|-1+0-6|

14

=

14

2

（2））

EB1

=（2，4，-2），

EA1

=（2，0，-2），

EH

=（-1，0，2），
设平面HB₁E的法向量为

m1

=（x，y，z）
则

m1 • EH =0 m1 • EB1 =0

即

2x+4y-2z=0 2x-2z=0

取x=2，则y=

1

2

，z=1．∴

m1

=（2，

1

2

，1）
令平面A₁B₁E的法向量为

m2

=（x，y，z）
则

m2 • EB1 =0 m2 • EA1 =0

取x=1，y=0，z=1，则为

m2

=（1，0，1）
∴|cos＜

m1

，

m2

＞|=

| m1 • m2 |

|m1| |m2 |

=

42

7

．
∵二面角H-B₁E-A为钝二面角．
∴二面角H-B₁E-A₁的平面角的余弦值为-

42

7

．