题目内容
已知函数![]() .(Ⅰ)求
.(Ⅰ)求![]() 的最小值;
的最小值;
(Ⅱ)当![]() 时,求证:
时,求证:![]() ≥
≥![]() .
.
解:(Ⅰ)∵![]() 且
且![]() ,当时,得
,当时,得![]() ……2分
……2分
当![]() 时,,
时,, ![]() 递减
递减
当![]() 时,,
时,,![]() 递增
递增
∴![]() 是
是![]() 的极小值点,也是最小值点.
的极小值点,也是最小值点.
∴![]() 的最小值为
的最小值为![]() ………………………………………………4分
………………………………………………4分
(Ⅲ)∵![]()
![]()
![]()
记![]() ,则
,则![]()
构造函数![]()
![]()
∴![]()
由![]() 得
得![]()
当![]() 时,,
时,,![]() 递减
递减
当![]() 时,
时,![]() ,
,![]() 递增
递增
∴![]() 时,
时,![]() 取最小值.
取最小值.
∴![]()
![]()
即:![]() ……………………………12分
……………………………12分

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
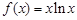 .
.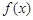 的最小值;
的最小值;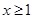 都有
都有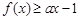 ,求实数
,求实数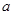 的取值范围.
的取值范围.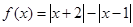
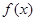 的值域;
的值域;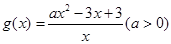 ,若对
,若对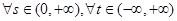 恒有
恒有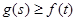 成立,试求实数
成立,试求实数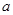 的取值氛围。
的取值氛围。 ,(1)求
,(1)求 的定义域;
的定义域; 是第四象限的角,且
是第四象限的角,且 ,求
,求 的值。
的值。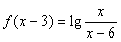 ,
,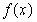 的解析式;
的解析式; .
.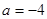 时,求
时,求 的最小值;
的最小值;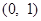 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;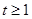 时,不等式
时,不等式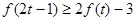 恒成立,求实数
恒成立,求实数