题目内容
对于定义域为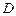 的函数
的函数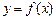 ,若有常数M,使得对任意的
,若有常数M,使得对任意的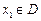 ,存在唯一的
,存在唯一的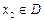 满足等式
满足等式 ,则称M为函数
,则称M为函数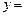 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数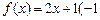 ≤
≤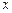 ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
解:(1)对任意的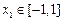 ,有
,有 ,
,
当且仅当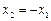 时,有
时,有 ,
,
故存在唯一 ,满足
,满足
 , ……………………2分
, ……………………2分
所以1是函数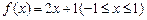 的“均值”. ……………………4分
的“均值”. ……………………4分
(另法:对任意的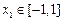 ,有
,有 ,令
,令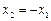 ,
,
则 ,且
,且 ,
,
若 ,且
,且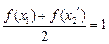 ,则有
,则有 ,可得
,可得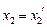 ,
,
故存在唯一 ,满足
,满足 , ……………………2分
, ……………………2分
所以1是函数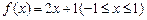 的“
的“ 均值”. ……………………4分)
均值”. ……………………4分)
(2)当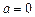 时,
时,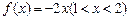 存在“均值”,且“均值”为
存在“均值”,且“均值”为 ;…………5分
;…………5分
当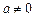 时,由
时,由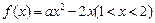 存在均值,可知对任意的
存在均值,可知对任意的 ,
,
都有唯一的 与之对应,从而有
与之对应,从而有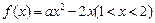 单调,
单调,
故有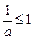 或
或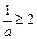 ,解得
,解得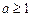 或
或 或
或 , ……………………9分
, ……………………9分
综上,a的取值范围是 或
或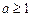 . ……………………10分
. ……………………10分
(另法:分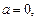
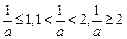 四种情形
四种情形 进行讨论)
进行讨论)
(3)①当I 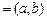 或
或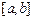 时,函数
时,函数 存在唯一的“均值”.
存在唯一的“均值”.
这时函数 的“均值”为
的“均值”为 ; …………………12分
; …………………12分
②当I为 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”.
这时任意实数均为函数 的“均值”; ……………………14分
的“均值”; ……………………14分
③当I  或
或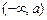 或
或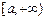 或
或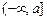 或
或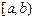 或
或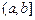 时,
时,
函数 不存在“均值”. ……………………16分
不存在“均值”. ……………………16分
[评分说明:若三种情况讨论完整且正确,但未用等价形式进行叙述,至多得6分;若三种情况讨论不完整,且未用等价形式叙述,至多得5分]
①当且仅当I形如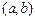 、
、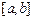 其中之一时,函数
其中之一时,函数 存在唯一的“均值”.
存在唯一的“均值”.
这时函数 的“均值”为
的“均值”为 ; ……………………13分
; ……………………13分
②当且仅当I为 时,函数
时,函数 存在无数多个“均值”.
存在无数多个“均值”.
这时任意实数均为函数 的“均值”;
的“均值”;
解析

 名校课堂系列答案
名校课堂系列答案 的函数
的函数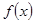 ,若存在区间
,若存在区间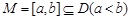 ,使得
,使得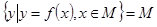 则称区间M为函数
则称区间M为函数 ; ②
; ②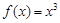 ; ③
; ③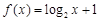
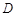 的函数
的函数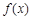 ,如果存在
,如果存在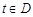 ,使得
,使得 成立,称函数
成立,称函数 ”函数。已知下列函数:①
”函数。已知下列函数:①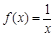 ; ②
; ②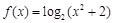 ;③
;③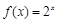 (
(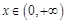 ); ④
); ④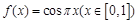 ,其中属于“
,其中属于“