题目内容
函数?（x）=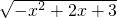
的递减区间是
- A.[1，3]
- B.（1，+∞）
- C.（-∞，3]
- D.（-∞，1]
A
分析：先求函数f（x）的定义域，函数f（x）可看作由y=
，t=-x2+2x+3复合而成的，因为y=单调递增，要求f（x）的减区间，只需求函数t=-x2+2x+3的减区间，在定义域内易求t=-x2+2x+3的减区间．
解答：由-x2+2x+3≥0解得-1≤x≤3，
所以函数f（x）的定义域为[-1，3]．
函数f（x）可看作由y=，t=-x2+2x+3复合而成的，
因为y=单调递增，要求f（x）的减区间，只需求函数t=-x2+2x+3的减区间，
而t=-x2+2x+3的减区间为[1，3]，
所以函数f（x）的减区间为[1，3]，
故选A．
点评：本题考查复合函数单调区间的求解及求函数的定义域，复合函数单调性的判断方法：先把复合函数进行“分解”，然后按照“同增异减”的原则判断即可，注意考虑函数定义域．
分析：先求函数f（x）的定义域，函数f（x）可看作由y=
，t=-x2+2x+3复合而成的，因为y=单调递增，要求f（x）的减区间，只需求函数t=-x2+2x+3的减区间，在定义域内易求t=-x2+2x+3的减区间．解答：由-x2+2x+3≥0解得-1≤x≤3，
所以函数f（x）的定义域为[-1，3]．
函数f（x）可看作由y=
，t=-x2+2x+3复合而成的，因为y=
单调递增，要求f（x）的减区间，只需求函数t=-x2+2x+3的减区间，而t=-x2+2x+3的减区间为[1，3]，
所以函数f（x）的减区间为[1，3]，
故选A．
点评：本题考查复合函数单调区间的求解及求函数的定义域，复合函数单调性的判断方法：先把复合函数进行“分解”，然后按照“同增异减”的原则判断即可，注意考虑函数定义域．
练习册系列答案
相关题目