题目内容
设复数z=3+i(i为虚数单位)在复平面中对应点A,将OA绕原点O逆时针旋转90°得到OB,则点B在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:由复数z求得点A的坐标,得到向量
的坐标,逆时针旋转90°,得到向量
的坐标,则B点坐标可求.
| OA |
| OB |
解答:
解:∵复数z=3+i(i为虚数单位)在复平面中对应点A(3,1),
∴
=(3,1),将
绕原点O逆时针旋转90°得到
,
设
=(a,b),则
,即
,解得:
或
.
∵是按逆时针方向旋转,
∴
=(-1,3),
∴B(-1,3).
∴点B在第二象限.
故选:B.
∴
| OA |
| OA |
| OB |
设
| OB |
|
|
|
|
∵是按逆时针方向旋转,
∴
| OB |
∴B(-1,3).
∴点B在第二象限.
故选:B.
点评:本题考查复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
设a,b,m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(modm).若a=
+
•2+
•22+…+
•220,a≡b(mod10),则b的值可以是( )
| C | 0 20 |
| C | 1 20 |
| C | 2 20 |
| C | 20 20 |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
某几何体的三视图如图所示,则该几何体的体积为( )


A、4
| ||||
B、
| ||||
C、
| ||||
| D、3 |
航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( )
| A、12种 | B、16种 |
| C、24种 | D、36种 |
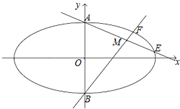 已知椭圆Γ:
已知椭圆Γ: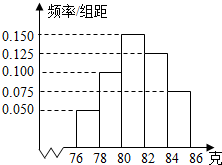 某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是
某厂对一批产品进行抽样检测,图2是抽检产品净重(单位:克)数据的频率分布直方图,样本数据分组为[76,78)、[78,80)、…、[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是