题目内容
已知椭圆C:
+y2=1及定点A(2,0),点P是椭圆上的动点,则|PA|的最小值为( )
| x2 |
| 9 |
分析:设出点P的坐标,求出|PA|,利用椭圆的方程,转化为二次函数,利用配方法,即可求得结论.
解答:解:设P(x,y),则|PA|2=(x-2)2+(y-0)2=x2-4x+4+y2
又∵(x,y)满足
+y2=1
∴|PA|2=x2-4x+4+y2=x2-4x+4+(1-
)=
x2-4x+5=
(x-
)2+
,其中-3≤x≤3
∵关于x的二次函数,开口向上,它的对称轴是x=
∴根据二次函数的性质,可知当x=
时,|PA|2取得最小值
∴|PA|的最小值为
故选A.
又∵(x,y)满足
| x2 |
| 9 |
∴|PA|2=x2-4x+4+y2=x2-4x+4+(1-
| x2 |
| 9 |
| 8 |
| 9 |
| 8 |
| 9 |
| 9 |
| 4 |
| 1 |
| 2 |
∵关于x的二次函数,开口向上,它的对称轴是x=
| 9 |
| 4 |
∴根据二次函数的性质,可知当x=
| 9 |
| 4 |
| 1 |
| 2 |
∴|PA|的最小值为
| ||
| 2 |
故选A.
点评:本题考查椭圆的标准方程,考查距离的计算,解题的关键是转化为二次函数,利用配方法求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
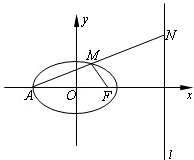 如图,已知椭圆
如图,已知椭圆