Question

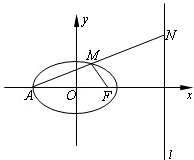如图，已知椭圆C：

x2

9

+

y2

5

=1的左顶点、右焦点分别为A、F，右准线为l，N为l上一点，且在x轴上方，AN与椭圆交于点M．
（1）若AM=MN，求证：AM⊥MF；
（2）设过A，F，N三点的圆与y轴交于P，Q两点，求PQ的最小值．

Answer 1

分析：（1）由题意及所给图形，先把点A，F具体，再把点N设出，利用条件解出t，求出k_AM•k_M若为-1，即可证明；
（2）由题意先设出圆的方程，在利用圆过A，F，N三点，写出圆的方程，由于圆与y轴交于P，Q两点，所以可以令圆的方程中x=0，写出两点坐标利用两点间的距离公式进而求解．

解答：（1）证明：由已知，A（-3，0），F（2，0），设N(

9

2

，t) (t＞0)，
则M(

3

4

，

t

2

)在椭圆C：

x2

9

+

y2

5

=1上，得t=

5 3

2

；
∴M(

3

4

，

5 3

4

)，∴kAM=kAN=

5 3 2

9 2 +3

=

3

3

，kMF=

5 3 4

3 4 -2

=-

3

，
∴k_AM•k_MF=-1，即AM⊥MF；
（2）解：设圆方程为x²+y²+dx+ey+f=0，将A，F，N三点的坐标代入得：

9-3d+f=0 4+2d+f=0 81 4 +t2+ 9 2 d+et+f=0

?

d=1 e=-t- 75 4t f=-6

，
∴圆方程为x2+y2+x-(t+

75

4t

)y-6=0，令x=0，得：y²+ey-6=0，
设P（0，y₁），Q（0，y₂），∴|PQ|=|y1-y2|=

(t+ 75 4t )2+24

≥3

11

，∴PQ的最小值为3

11

．

点评：（1）此问重点考查了利用方程的思想，还考查了利用两条直线的斜率互为负倒数证明直线垂直；
（2）此问重点考查了利用方程的思想进行求解，还考查了利用一元二次函数求解最值及两点间的距离公式．