题目内容
已知α,β∈(
,π),且tanα+tan(β-
)>0,则必有( )
| π |
| 2 |
| π |
| 2 |
A、α+β>
| ||
B、α+β<
| ||
C、α+β=
| ||
| D、α-β>0 |
分析:把已知的不等式左边利用诱导公式及同角三角函数间的基本关系变形,根据β的范围得到tanβ小于0,不等式两边同时乘以tanβ,不等号方向改变,得到1-tanαtanβ的值小于0,又根据α的范围得到tanα的值也小于0,进而得到tanα+tanβ的值小于0,最后利用两角和与差的正切函数公式表示出tan(α+β),利用1-tanαtanβ及tanα+tanβ的符号判断得到其值小于0,根据α+β的范围,利用正切函数的图象即可得到α+β的具体范围.
解答:解:∵tanα+tan(β-
)=tanα-cotβ>0,即tanα>cotβ=
,
又β∈(
,π),∴tanβ<0,
∴1-tanαtanβ<0,又α∈(
,π),得到tanα<0,即tanα+tanβ<0,
∴tan(α+β)=
<0,又α+β∈(π,2π),
则必有α+β>
.
故选A
| π |
| 2 |
| 1 |
| tanβ |
又β∈(
| π |
| 2 |
∴1-tanαtanβ<0,又α∈(
| π |
| 2 |
∴tan(α+β)=
| tanα+tanβ |
| 1-tanαtanβ |
则必有α+β>
| 3π |
| 2 |
故选A
点评:此题考查了诱导公式,同角三角函数间的基本关系,正切函数的图象与性质以及两角和与差的正切函数公式,熟练掌握公式是解本题的关键,同时注意角度的范围.

练习册系列答案
相关题目
 已知定点A
已知定点A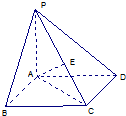 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知:PA=2,AB=2,
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知:PA=2,AB=2,