题目内容
若 、
、 为双曲线
为双曲线 :
:  的左、右焦点,点
的左、右焦点,点 在双曲线
在双曲线 上,∠
上,∠ =
= ,则
,则 到
到 轴的距离为( )
轴的距离为( )
A. | B. | C. | D. |
B
解析试题分析:双曲线: ,
,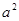 =4,
=4,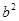 =1,
=1,
所以a=2,b=1。c²=a²+b²=5,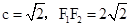 ,
,
根据题意|P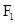 -P
-P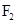 |=2a=4,P
|=2a=4,P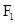 ²+P
²+P 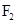 ²-2P
²-2P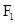 ·P
·P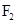 =16,
=16,
由余弦定理得,cos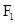 P
P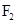 =
=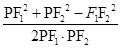 ,
,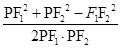
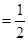 ,
,
由正弦定理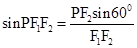 ,
,
P到x轴距离=  =
=
故选B。
考点:双曲线的定义及其几何性质,正弦定理、余弦定理的应用。
点评:中档题,本题综合性较强,综合考查双曲线的定义及其几何性质,正弦定理、余弦定理的应用。注意数形结合,利用图形发现边角关系。

练习册系列答案
相关题目
经过点 ,渐近线与圆
,渐近线与圆 相切的双曲线的标准方程为( )
相切的双曲线的标准方程为( )
A. | B. | C. | D.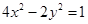 |
已知两个正数 ,
, 的等差中项是
的等差中项是 ,一个等比中项是
,一个等比中项是 ,且
,且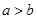 ,则抛物线
,则抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C. | D. |
设抛物线 上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )
上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )
| A.4 | B.6 | C.8 | D.12 |
若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )
A. | B. | C. | D. |
已知三个数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B. | C. 或 或 | D. 或 或 |
(5分)抛物线y2=8x的焦点到直线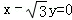 的距离是( )
的距离是( )
A. | B.2 | C. | D.1 |
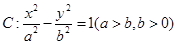 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若 ,则双曲线的离心率是( )
,则双曲线的离心率是( )


 是双曲线
是双曲线 左支上一点,该双曲线的一条渐近线方程是
左支上一点,该双曲线的一条渐近线方程是 ,
, 分别是双曲线的左、右焦点,若
分别是双曲线的左、右焦点,若 ,则
,则 等于( )
等于( )