题目内容
已知抛物线y=ax2-1上存在关于直线l:x+y=0成轴对称的两点,试求实数a的取值范围.
解法一:设抛物线上关于直线l对称的两相异点为P(x1,y1)、Q(x2,y2),线段PQ的中点为M(x0,y0),设直线PQ的方程为y=x+b,由于P、Q两点存在,所以方程组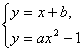 有两组不同的实数解,即得方程ax2-x-(1+b)=0. ①
有两组不同的实数解,即得方程ax2-x-(1+b)=0. ①
判别式Δ=1+4a(1+b)>0. ②
由①得x0=![]() =
=![]() ,y0=x0+b=
,y0=x0+b=![]() +b.
+b.
∵M∈l,∴0=x0+y0=![]() +
+![]() +b,即b=-
+b,即b=-![]() ,代入②解得a>
,代入②解得a>![]() .
.
解法二:设同解法一,由题意得
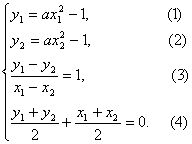
将①②代入③④,并注意到a≠0,x1-x2≠0,
得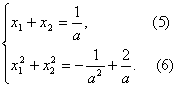
由二元均值不等式易得
2(x12+x22)>(x1+x2)2(x1≠x2).
将⑤⑥代入上式得
2(-![]() +
+![]() )>(
)>(![]() )2,解得a>
)2,解得a>![]() .
.
解法三:同解法二,由①-②,得
y1-y2=a(x1+x2)(x1-x2).
∵x1-x2≠0,
∴a(x1+x2)=![]() =1.
=1.
∴x0=![]() =
=![]() .
.
∵M(x0,y0)∈l,
∴y0+x0=0,即y0=-x0=-![]() ,从而PQ的中点M的坐标为(
,从而PQ的中点M的坐标为(![]() ,-
,-![]() ).
).
∵M在抛物线内部,
∴a(![]() )2-(-
)2-(-![]() )-1<0.
)-1<0.
解得a>![]() .(舍去a<0,为什么?).
.(舍去a<0,为什么?).

练习册系列答案
相关题目
已知抛物线y=ax2+bx+c与直线y=-bx交于A、B两点,其中a>b>c,a+b+c=0,设线段AB在x轴上的射影为A1B1,则|A1B1|的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(2, 2
|