题目内容
设点P在曲线y=
ex+1上,点Q在曲线y=ln(2x-2)上,则|PQ|最小值为( )
| 1 |
| 2 |
| A、1-ln2 | ||
B、
| ||
| C、1+ln2 | ||
D、
|
分析:根据函数y=
ex+1与函数y=ln(2x-2)互为反函数,可知P、Q两点间的最短距离为点P到直线y=x的最短距离d的2倍,利用导数求出d即可.
| 1 |
| 2 |
解答:解:∵函数y=
ex+1与函数y=ln(2x-2)互为反函数,
∴函数y=
ex+1与函数y=ln(2x-2)的图象关于直线y=x对称,
∴|PQ|的最小值是点P到直线y=x的最短距离的2倍,
设曲线y=
ex+1上斜率为1的切线为y=x+b,
∵y′=
ex,由
ex=1得x=ln2,
即切点为(ln2,2),
∴b=2-ln2,
∴d=
,
∴P、Q两点间的最短距离为2d=
(2-ln2),
故选B.
| 1 |
| 2 |
∴函数y=
| 1 |
| 2 |
∴|PQ|的最小值是点P到直线y=x的最短距离的2倍,
设曲线y=
| 1 |
| 2 |
∵y′=
| 1 |
| 2 |
| 1 |
| 2 |
即切点为(ln2,2),
∴b=2-ln2,
∴d=
| |2-ln2| | ||
|
∴P、Q两点间的最短距离为2d=
| 2 |
故选B.
点评:本题考查反函数的概念,导数的几何意义,点到直线的距离公式等式知识的灵活应用,属于难题.

练习册系列答案
相关题目

 在平面直角坐标系xoy中,设点
在平面直角坐标系xoy中,设点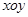 中,已知三点
中,已知三点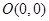 ,
,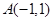 ,
,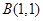 ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: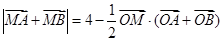 .
.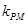 ,
,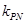 .试探究
.试探究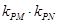 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论; 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.