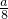题目内容
设F为拋物线y2=ax(a>0)的焦点,点P在拋物线上,且其到y轴的距离与到点F的距离之比为1:2,则|PF|等于( )A.

B.a
C.

D.

【答案】分析:依题意,设P(x,y),利用拋物线定义知|PF|=x+ ,点P到y轴的距离与到点F的距离之比为1:2,列式得
,点P到y轴的距离与到点F的距离之比为1:2,列式得 =
= ,可求得x,继而可得答案.
,可求得x,继而可得答案.
解答:解:设P(x,y),则y2=ax,
由拋物线定义知|PF|=x+ ,
,
由已知得 =
= ,解得x=
,解得x= ,
,
∴|PF|= +
+ =
= .
.
故选D.
点评:本题考查抛物线的简单性质,考查待定系数法,考查理解与运算能力,属于中档题.
 ,点P到y轴的距离与到点F的距离之比为1:2,列式得
,点P到y轴的距离与到点F的距离之比为1:2,列式得 =
= ,可求得x,继而可得答案.
,可求得x,继而可得答案.解答:解:设P(x,y),则y2=ax,
由拋物线定义知|PF|=x+
 ,
,由已知得
 =
= ,解得x=
,解得x= ,
,∴|PF|=
 +
+ =
= .
.故选D.
点评:本题考查抛物线的简单性质,考查待定系数法,考查理解与运算能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目