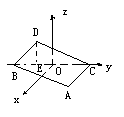题目内容
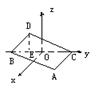
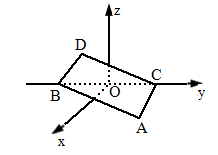
如下图，在空间直角坐标系中
BC=2，原点O是BC的中点，点A的坐标是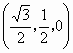
，点D在平面yOz上，且∠BDC=90°，∠DCB=30°．
(1)
求向量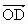
的坐标；
(2)
设向量
和
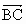的夹角为θ，求cosθ的值．
答案：略
解析：
解析：
|
(1)过 D作DE⊥BC，垂足为E，在 Rt△BDC中，由∠BDC=90°，∠DCB=30°，BC=2，得BD=1， ，∴ ．
所以  ．
∴ D点坐标为 ，即向量 的坐标 ．
(2) 依题意：  ， ， ，
所以  ， ．
设向量  和 的夹角为θ，则 ． |
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
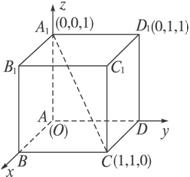
如图，在空间直角坐标系中，正方体棱长为2，点E是棱AB的中点，点F（0，y，z）是正方体的面AA1D1D上点，且CF⊥B1E，则点F（0，y，z）满足方程（ ）| A、y-z=0 | B、2y-z-1=0 | C、2y-z-2=0 | D、z-1=0 |
，
，0），点D在平面yoz上，且
BDC=900，
，
，0），点D在平面yoz上，且
BDC=900，
