题目内容
命题“对任意的 ,都有
,都有 ”的否定为( )
”的否定为( )
A.存在 ,使 ,使 |
B.对任意的 ,都有 ,都有 |
C.存在 ,使 ,使 |
D.存在 ,使 ,使 |
C
解析试题分析:因为全称命题的否定为特称命题,所以命题“对任意的 ,都有
,都有 ”的否定为存在
”的否定为存在 ,使
,使 。
。
考点:全称命题的否定。
点评:本题考查的知识点是命题的否定,其中熟练掌握全称命题的否定方法“?x∈A,p(x)”的否定是“?x∈A,非p(x)”,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“ ”是“直线
”是“直线 和
和 平行”的( )
平行”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
某学习小组对函数 进行研究,得出了如下四个结论:①函数
进行研究,得出了如下四个结论:①函数 在
在 上单调递增;②存在常数
上单调递增;②存在常数 对一切实数
对一切实数 均成立;③函数
均成立;③函数 在
在 上无最小值,但一定有最大值;④点
上无最小值,但一定有最大值;④点 是函数
是函数 的一个对称中心,其中正确的是
的一个对称中心,其中正确的是
| A.①③ | B.②③ | C.②④ | D.①②④ |
“ ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( )
| A.充分必要条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |
若命题“
 时,
时, ”是假命题,则
”是假命题,则 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
已知命题p: ,则
,则 为( )。
为( )。
A. , , | B.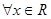 , , |
C. , , | D.: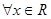 , , |
命题“对任意的 ”的否定是( )
”的否定是( )
A.不存在 | B.存在 |
C.存在 | D.对任意的 |
 是“直线
是“直线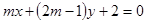 和直线
和直线 垂直”的( )
垂直”的( )
| A.必要而不充分条件 | B.充分而不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
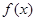 的定义域为D,若存在非零实数
的定义域为D,若存在非零实数 使得对于任意
使得对于任意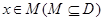 ,有
,有 ,且
,且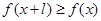 ,则称
,则称 为R上的1高调函数;
为R上的1高调函数;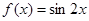 为R上的
为R上的 高调函数;
高调函数; 的函数
的函数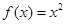 为
为 高调函数,那么实数
高调函数,那么实数 ;
; 为
为 上的2高调函数。
上的2高调函数。